题目内容
18.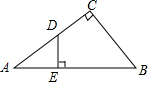 在△ABC中,∠ACB=90°,DE⊥AB.
在△ABC中,∠ACB=90°,DE⊥AB.(1)指出图中的相似三角形?并说明理由.
(2)若分别延长DE,BC交于点F,这时,图中还有哪些三角形相似?
(3)若连接EC、AF,这时,图中还有哪些三角形也相似?
(4)若∠B=60°,AF=6,求CE长.
分析 (1)根据两角对应相等两三角形相似,可得△AED∽△ACB;
(2)根据两角对应相等,则△ADE∽△FDC∽△FBE∽△ABC;
(3)根据△ACB∽△FEB,得夹∠B的两边对应成比例,所以又得△CEB∽△AFB;
(4)根据直角三角形30°角的性质得:$\frac{AB}{CB}=2$,由△CEB∽△AFB,得$\frac{AF}{CE}=\frac{AB}{CB}$=2,可以求出CE的长.
解答 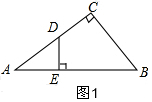 解:(1)△AED∽△ACB,理由是:
解:(1)△AED∽△ACB,理由是:
∵DE⊥AB,
∴∠AED=90°,
∵∠ACB=90°,
∴∠AED=∠ACB,
∵∠A=∠A,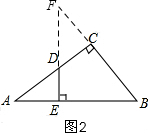
∴△AED∽△ACB;
(2)还有以下三角形相似:如图2,
①△ADE∽△FDC,理由是:
∵∠ADE=∠FDC,∠AED=∠DCF=90°,
∴△ADE∽△FDC,
∴∠A=∠F;
②△ACB∽△FEB,理由是:
∵∠A=∠F,∠B=∠B,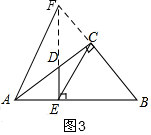
∴△ACB∽△FEB;
③△FDC∽△FBE,理由是:
∵∠F=∠F,∠DCF=∠BEF,
∴△FDC∽△FBE;
④△AED∽△FEB,理由是:
∵∠A=∠F,∠AED=∠FEB=90°,
∴△AED∽△FEB;
⑤△FDC∽△ABC,理由是:
∵∠A=∠F,∠FCD=∠ACB,
∴△FDC∽△ABC;
(3)还有△CEB∽△AFB,理由是:
∵△ACB∽△FEB,
∴$\frac{AB}{FB}=\frac{CB}{EB}$,
∴$\frac{AB}{CB}=\frac{FB}{EB}$,
∵∠B=∠B,
∴△CEB∽△AFB;
(4)在Rt△ACB中,∠B=60°,
∴∠CAB=30°,
∴AB=2CB,
∴$\frac{AB}{CB}$=2,
∵△CEB∽△AFB,
∴$\frac{AF}{CE}=\frac{AB}{CB}$=2,
∵AF=6,
∴CE=3.
点评 本题考查了三角形相似的性质和判定,三角形相似常运用两角对应相等这一方法来判定,除了两角对应相等外,还应掌握其它判定方法:①平行相似,②两边对应成比例,且夹角相等,两三角形相似,③三边对应成比例,两三角形相似.

| A. | a=3,b=4,c=5 | B. | a=2,b=3,c=4 | C. | a=5,b=12,c=13 | D. | a=8,b=15,c=17 |
| A. | 是平行四边形 | B. | 一定是正方形 | C. | 可能是菱形 | D. | 必是矩形 |
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定形状 |
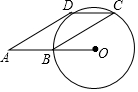 如图,A为⊙O外一点交⊙O于点B,C、D为⊙O上的两点,AD为⊙O的切线,若四边形ABCD为平行四边形,则∠A的度数为30°.
如图,A为⊙O外一点交⊙O于点B,C、D为⊙O上的两点,AD为⊙O的切线,若四边形ABCD为平行四边形,则∠A的度数为30°.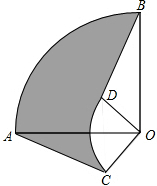 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC、BD,若OA=6cm,OC=2cm,则阴影部分的面积为8πcm2.
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC、BD,若OA=6cm,OC=2cm,则阴影部分的面积为8πcm2.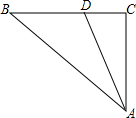 Rt△ABC中,∠C=90°,AC=3,BC=4,动点D在边BC上从点C向点B运动,连接AD,点C关于直线AD的对称点为点P,若△BCP为等腰三角形,则CP2的值为16或18-6$\sqrt{5}$或$\frac{576}{25}$.
Rt△ABC中,∠C=90°,AC=3,BC=4,动点D在边BC上从点C向点B运动,连接AD,点C关于直线AD的对称点为点P,若△BCP为等腰三角形,则CP2的值为16或18-6$\sqrt{5}$或$\frac{576}{25}$.