题目内容
15.如图1,线段AB的端点在正方形网格的格点上,在图1中找到格点C,使组成的△ABC的一个内角α满足tanα=2(找到两个点C,全等的三角形算一种).(2)如图2,在Rt△DEF中,∠DEF=90°,DE=1,sin∠F=$\frac{\sqrt{10}}{10}$.用两块全等的△DEF拼出一个平行四边形,将拼得的平行四边形画在图2网格(网格图中小正方形边长均为1)中,画出不同的两种平行四边形(全等的算一种),并写出相应的周长.
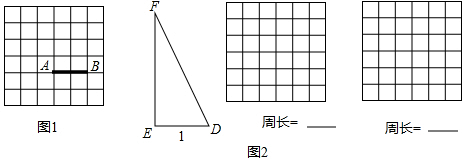
分析 (1)根据题意,所画的直角三角形的直角边之间是两倍关系即可;
(2)有三种拼法,分别求出周长即可;
解答 解:(1)如图△ABC,△ABC′即为所求;
(2)有三种拼法:周长分别为8,2+2$\sqrt{10}$,6+2$\sqrt{10}$.
点评 本题考查作图-应用与设计、勾股定理、平行四边形的判定和性质.解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
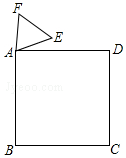 如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小是15°或165°.
如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小是15°或165°.
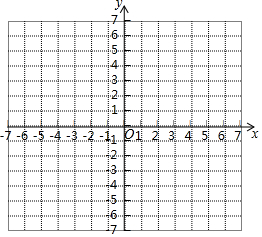 在如图所示平面直角坐标系中,已知A(-2,2),B(-3,-2),C(3,-2).
在如图所示平面直角坐标系中,已知A(-2,2),B(-3,-2),C(3,-2).