题目内容
4.若ax=2,ay=3,则a3x-2y=$\frac{8}{9}$.若a-b=-2,则$\frac{1}{2}$(a2+b2)-ab=2.
分析 (1)根据同底数幂的运算法则即可求出答案.
(2)根据完全平方公式即可求出答案.
解答 解:(1)∵ax=2,ay=3
∴a3x-2y=a3x÷a2y=(ax)3÷(ay)2=8÷9=$\frac{8}{9}$
(2)∵a-b=-2
∴a2-2ab+b2=4,
∴a2+b2=4+2ab,
∴原式=$\frac{1}{2}$(4+2ab)-ab=2
故答案为:(1)$\frac{8}{9}$;(2)2
点评 本题考查学生的运算能力,解题的关键熟练运用运算法则,本题属于基础题型.

练习册系列答案
相关题目
14.等边三角形ABC的边长AB=10cm,则这个三角形的BC边上的高为( )cm.
| A. | $\sqrt{50}$ | B. | $\sqrt{95}$ | C. | $\sqrt{15}$ | D. | $\sqrt{75}$ |
9.已知函数y=2x+b的图象过点(2,3),当 x=3时,y的值是( )
| A. | 4 | B. | 5 | C. | 8 | D. | 7 |
16.若一个三角形的三边长分别为5、7、x-2,则x的取值范围是( )
| A. | 0<x<14 | B. | 4<x<14 | C. | 0<x<10 | D. | 2<x<10 |
13.若a,b为两质数且相差2,则ab+1之值可能为下列何者( )
| A. | 392 | B. | 402 | C. | 412 | D. | 422 |
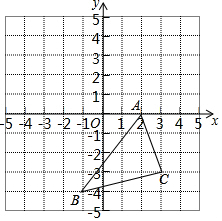 在如图所示的直角坐标系中,解答下列问题:
在如图所示的直角坐标系中,解答下列问题: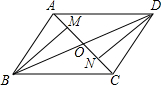 已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,M、N分别是OA、OC的中点,求证:BM∥DN.
已知:如图,平行四边形ABCD的对角线AC、BD相交于点O,M、N分别是OA、OC的中点,求证:BM∥DN.