题目内容
5.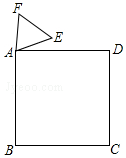 如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小是15°或165°.
如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小是15°或165°.
分析 先根据BE=DF,AE=AF,AB=AD判定△ABE≌△ADF,再根据∠BAE的位置求得其度数.
解答 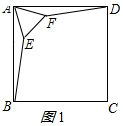 解:∵四边形ABCD是正方形,
解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵△AEF是等边三角形,
∴AE=AF,∠EAF=60°,
分两种情况:
①如图,当正△AEF在正方形ABCD内部时,
在△ABE和△ADF中,$\left\{\begin{array}{l}{BE=DF}&{\;}\\{AE=AF}&{\;}\\{AB=AD}&{\;}\end{array}\right.$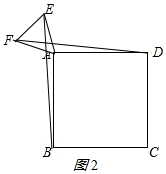
∴△ABE≌△ADF(SSS),
∴∠BAE=∠DAF=$\frac{1}{2}$(90°-60°)=15°
②如图,当正△AEF在正方形ABCD外部时,
在△ABE和△ADF中,$\left\{\begin{array}{l}{BE=DF}&{\;}\\{AE=AF}&{\;}\\{AB=AD}&{\;}\end{array}\right.$
∴△ABE≌△ADF(SSS),
∴∠BAE=∠DAF=$\frac{1}{2}$(360°-90°+60°)=165°
故答案为:15°或165°.
点评 本题主要考查了正方形和等边三角形的性质,解决问题的关键是掌握全等三角形的判定与性质.在求∠BAE的度数时,需要分两种情况进行讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.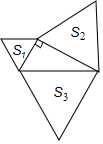 如图,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3.其中S1=4,S2=12,则S3=( )
如图,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3.其中S1=4,S2=12,则S3=( )
 如图,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3.其中S1=4,S2=12,则S3=( )
如图,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3.其中S1=4,S2=12,则S3=( )| A. | 8 | B. | 16 | C. | 160 | D. | 128 |
14.等边三角形ABC的边长AB=10cm,则这个三角形的BC边上的高为( )cm.
| A. | $\sqrt{50}$ | B. | $\sqrt{95}$ | C. | $\sqrt{15}$ | D. | $\sqrt{75}$ |
 如图,AB是⊙O的直径,点C是半圆上的一个三等分点,点D是$\widehat{AC}$的中点,点P是直径AB上一点,若⊙O的半径为2,则PC+PD的最小值是2$\sqrt{2}$.
如图,AB是⊙O的直径,点C是半圆上的一个三等分点,点D是$\widehat{AC}$的中点,点P是直径AB上一点,若⊙O的半径为2,则PC+PD的最小值是2$\sqrt{2}$.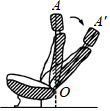 这是一把可调节座椅的侧面示意图,已知头枕上的点A到调节器点O处的距离为80 cm,AO与地面垂直.现调节靠背,把OA绕点O旋转35°到OA'处.则调整后点A'比调整前点A的高度降低了14厘米.(结果取整数,参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
这是一把可调节座椅的侧面示意图,已知头枕上的点A到调节器点O处的距离为80 cm,AO与地面垂直.现调节靠背,把OA绕点O旋转35°到OA'处.则调整后点A'比调整前点A的高度降低了14厘米.(结果取整数,参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70) 如图,EA∥BD,∠BAC=∠BCA,∠ACD=110°,求∠EAB的度数.
如图,EA∥BD,∠BAC=∠BCA,∠ACD=110°,求∠EAB的度数.