题目内容
18.在菱形ABCD中,对角线AC,BD交于点O,∠ABC=120°,周长为16,则OD=2.分析 根据菱形的四条边都相等求出菱形的边长,再根据菱形的邻角互补求出∠BAD=60°,然后求出△ABD是等边三角形,从而得到BD的长,根据菱形的对角线互相平分求出OD的长.
解答  解:∵菱形ABCD的周长为16,
解:∵菱形ABCD的周长为16,
∴AB=BC=CD=DA=16÷4=4,AB∥CD,
∵∠ABC=120°,
∴∠BAD=60°,
∴△ABD是等边三角形,
∴BD=AB=AD=4,
∵菱形ABCD对角线AC、BD相交于点O,
∴OD=$\frac{1}{2}$BD=2.
故答案为2.
点评 本题考查了菱形的性质,主要利用了菱形的四条边都相等,邻角互补,对角线互相平分的性质,证明得到△ABD是等边三角形是解题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
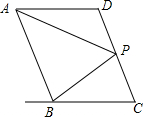 如图,已知AD∥BC,AP平分∠BAD,BP平分∠ABC,点P恰好在DC上,下面结论:①AP⊥BP,②点P到直线AD,BC的距离相等,③PD=PC,其中结论正确的是①②③.
如图,已知AD∥BC,AP平分∠BAD,BP平分∠ABC,点P恰好在DC上,下面结论:①AP⊥BP,②点P到直线AD,BC的距离相等,③PD=PC,其中结论正确的是①②③.