题目内容
13.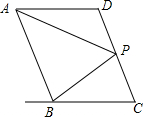 如图,已知AD∥BC,AP平分∠BAD,BP平分∠ABC,点P恰好在DC上,下面结论:①AP⊥BP,②点P到直线AD,BC的距离相等,③PD=PC,其中结论正确的是①②③.
如图,已知AD∥BC,AP平分∠BAD,BP平分∠ABC,点P恰好在DC上,下面结论:①AP⊥BP,②点P到直线AD,BC的距离相等,③PD=PC,其中结论正确的是①②③.
分析 作PE⊥AD交AD的延长线于E,PF⊥BC于F,PG⊥AB于G,根据角平分线的定义和平行线的性质证明①正确;根据角平分线的性质证明②正确;运用全等三角形的判定定理和性质定理证明③正确.
解答 解:作PE⊥AD交AD的延长线于E,PF⊥BC于F,PG⊥AB于G,
∵AD∥BC,
∴∠DAB+∠ABC=180°,
∵AP平分∠DAB,BP平分∠ABC,
∴∠PAB=$\frac{1}{2}$∠DAB,∠PBA=$\frac{1}{2}$∠ABC,
∴∠PAB+∠PBA=90°,
∴∠APB=90°,即AP⊥BP,①正确;
∵AP平分∠DAB,PE⊥AD,PG⊥AB,
∴PE=PG,
同理,PF=PG,
∴PE=PF,即点P到直线AD、BC的距离相等,②正确;
由题意得,△DPE≌△CPF,
∴PD=PC,③正确,
故答案为:①②③.
点评 本题考查的是角平分线的定义和性质以及平行线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
8.关于x的分式方程$\frac{3}{x}$+$\frac{6}{x-1}$-$\frac{x+k}{x(x-1)}$=0有解,则k满足( )
| A. | k≠-3 | B. | k≠5 | C. | k≠-3且k≠-5 | D. | k≠-3且k≠5 |
5.化简分式:$\frac{x-\frac{1}{y}}{y-\frac{1}{x}}$等于( )
| A. | 1 | B. | $\frac{y}{x}$ | C. | $\frac{x}{y}$ | D. | $\frac{x}{y}-\frac{y}{x}$ |
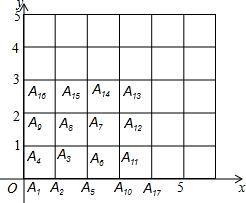 如图所示,已知点A1的坐标为(0,0),点A2的坐标为(1,0),点A3的坐标为(1,1),点A4的坐标为(0,1),A5的坐标为(2,0),点A6坐标为(2,1),点A7的坐标为(2,2),点A8的坐标为(1,2),点A9的坐标为(0,2),点A10的坐标为(3,0),点A11的坐标为(3,1),…,依此规律排列下去,则点A25的坐标为(0,4),点A2015的坐标为(34,44).
如图所示,已知点A1的坐标为(0,0),点A2的坐标为(1,0),点A3的坐标为(1,1),点A4的坐标为(0,1),A5的坐标为(2,0),点A6坐标为(2,1),点A7的坐标为(2,2),点A8的坐标为(1,2),点A9的坐标为(0,2),点A10的坐标为(3,0),点A11的坐标为(3,1),…,依此规律排列下去,则点A25的坐标为(0,4),点A2015的坐标为(34,44).