题目内容
8.已知n个数x1,x2,…,xn,每个数只能取0,1,-1中的一个,若x1+x2+…+xn=2016,则x12015+x22015+…+xn2015的值为2016.分析 根据题意可设这列数中有a个0、b个1、c个-1,由x1+x2+…+xn=2016可得b-c=2016,而x12015+x22015+…+xn2015的值与x1+x2+…+xn相同,可得答案.
解答 解:∵n个数x1,x2,…,xn每个数只能取0,1,-1中的一个,
∴设这列数中有a个0,b个1,c个-1,
则0•a+1•b+(-1)•c=2016,即:b-c=2016,
∴x12015+x22015+…+xn2015=0•a+1•b+(-1)•c=b-c=2016,
故答案为:2016.
点评 本题主要考查数字的变化类,根据题意找到待求代数式与已知数列间的联系是解题的关键.

练习册系列答案
相关题目
18.将分式方程$\frac{3}{4x-2}$-$\frac{2x}{2-4x}$=1去分母正确的是( )
| A. | 3+2x=1 | B. | 3(2-4x)-2x(4x-2)=1 | ||
| C. | 3(2-4x)+2x(4x-2)=4x-2 | D. | 3+2x=4x-2 |
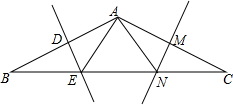 在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.
在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.