题目内容
11.已知:在?ABCD中,点M是BC的中点,∠MDA=∠MAD.求证:?ABCD是矩形.分析 由平行四边形的性质得出AB=DC,AB∥DC,得出∠B+∠C=180°,证出BM=CM,AM=DM,由SSS证明△ABM≌△DCM,得出∠B=∠C,证出∠B=∠C=90°,即可得出结论.
解答 证明:如图所示: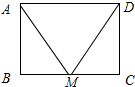
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠B+∠C=180°,
∵M是BC的中点,
∴BM=CM,
∵∠MDA=∠MAD,
∴AM=DM,
在△ABM和△DCM中,
$\left\{\begin{array}{l}{AB=DC}&{\;}\\{BM=CM}&{\;}\\{AM=DM}&{\;}\end{array}\right.$,
∴△ABM≌△DCM(SSS),
∴∠B=∠C,
∴∠B=∠C=90°,
∴?ABCD是矩形.
点评 此题主要考查了矩形的判定、平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等得出对应角相等是解决问题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
19.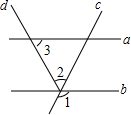 如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )
如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )
 如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )
如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
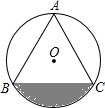 如图,已知边长为6的等边△ABC内接于⊙O.
如图,已知边长为6的等边△ABC内接于⊙O.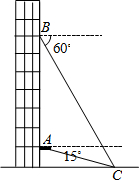 从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图,直线AB与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)
从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图,直线AB与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)