题目内容
7.已知四位数x是完全平方数,将其4个数字各加1后得到的四位数仍然是完全平方数,则x=2025.分析 设x=a2①,则x+1111=b2②,将②-①,得出b2-a2=1111,由于1111=101×11,那么(b+a)(b-a)=101×11,从而得出方程组$\left\{\begin{array}{l}{b+a=101}\\{b-a=11}\end{array}\right.$,解方程组求出a、b的值即可.
解答 解:设x=a2①,则x+1111=b2②,
②-①,得b2-a2=1111,
即:(b+a)(b-a)=101×11,
所以 $\left\{\begin{array}{l}{b+a=101}\\{b-a=11}\end{array}\right.$,
解这个方程组,得$\left\{\begin{array}{l}{a=45}\\{b=56}\end{array}\right.$,
所以x=a2=452=2025,b2=562=3136.
所以这个四位数是2025.
故答案为2025.
点评 本题考查了完全平方数,平方差公式,设x=a2,则x+1111=b2,得出方程组$\left\{\begin{array}{l}{b+a=101}\\{b-a=11}\end{array}\right.$是解题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
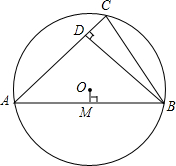 如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,OM的长为0.3,求sin∠CBD的值.
如图,已知⊙O的半径为1,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,OM的长为0.3,求sin∠CBD的值.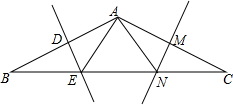 在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.
在△ABC中,AB=AC,BC=12,∠B=30°,AB的垂直平分线DE交BC边于点E,AC的垂直平分线MN交BC于点N.