题目内容
10．已知$\frac{1}{x}$+$\frac{1}{y}$=3，求分式$\frac{3x-2xy+3y}{x+xy+y}$的值．分析 首先将已知变形进而得出x+y=3xy，再代入原式求出答案．
解答 解：∵$\frac{1}{x}$+$\frac{1}{y}$=3，
∴$\frac{x+y}{xy}$=3，
则x+y=3xy，
∴$\frac{3x-2xy+3y}{x+xy+y}$=$\frac{3（x+y）-2xy}{（x+y）+xy}$=$\frac{9xy-2xy}{3xy+xy}$=$\frac{7}{4}$．
点评 此题主要考查了分式的值，正确将已知变形进而化简是解题关键．
练习册系列答案
导学教程高中新课标系列答案
相关题目
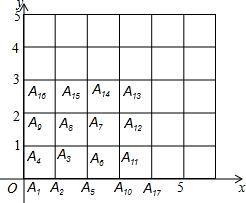如图所示，已知点A1的坐标为（0，0），点A2的坐标为（1，0），点A3的坐标为（1，1），点A4的坐标为（0，1），A5的坐标为（2，0），点A6坐标为（2，1），点A7的坐标为（2，2），点A8的坐标为（1，2），点A9的坐标为（0，2），点A10的坐标为（3，0），点A11的坐标为（3，1），…，依此规律排列下去，则点A25的坐标为（0，4），点A2015的坐标为（34，44）．
5．化简分式：$\frac{x-\frac{1}{y}}{y-\frac{1}{x}}$等于（ ）
| A． | 1 | B． | $\frac{y}{x}$ | C． | $\frac{x}{y}$ | D． | $\frac{x}{y}-\frac{y}{x}$ |
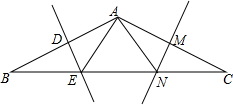在△ABC中，AB=AC，BC=12，∠B=30°，AB的垂直平分线DE交BC边于点E，AC的垂直平分线MN交BC于点N．