题目内容
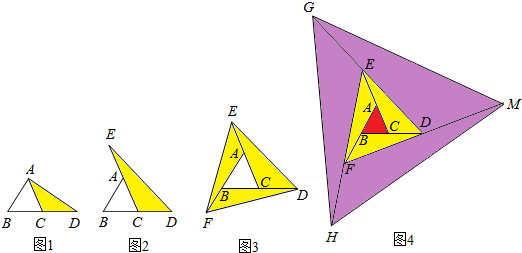
13.在图1到图4中,已知△ABC的面积为m.(1)如图1,延长△ABC的边BC到点D使CD=BC,连接DA,若△ACD的面积为S1,则S1=m.(用含m的式子表示)
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S2,则S2=2m.(用含m的代数式表示)
(3)如图3,在图2的基础上延长AB到点F,使BF=AB,连接FD于E,得到△DEF,若阴影部分的面积为S3,则S3=6m.(用含m的代数式表示)并运用上述2的结论写出理由.
(4)可以发现将△ABC各边均顺次延长一倍,连接所得端点,得到△DEF,如图3,此时,我们称△ABC向外扩展了一次.可以发现扩展一次后得到的△DEF的面积是原来△ABC面积的7倍.
(5)应用上面的结论解答下面问题:
去年在面积为15平方面的△ABC空地上栽种了各种花卉,今年准备扩大种植规模,把△ABC内外进行两次扩展,第一次由△ABC扩展成△DEF,第二次由△DEF扩展成△MGH,如图4,求这两次扩展的区域(即阴影部分)面积共为多少平方米?
分析 (1)利用三角形的面积公式,等底同高的三角形面积相等,本题得以解决.
(2)利用三角形的面积公式,等底同高的三角形面积相等,本题得以解决.
(3)利用三角形的面积公式,等底同高的三角形面积相等,本题得以解决.
(4)利用三角形的面积公式,等底同高的三角形面积相等,本题得以解决.
(5)根据第四问的经验,得出扩展一次面积变为原来的7倍,得出两次扩展面积,本题得以解决
解答 解:(1)∵CD=BC,
∴△ABC和△ACD的面积相等(等底同高),
∴得出结论S1=m.
故答案为m.
(2)如图2,连接AD,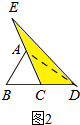
∵AE=CA,
∴△DEC的面积S2为△ACD的面积S1的2倍,
∴得出结论S2=2m.
故答案为2m
(3)结合(1)(2)得出阴影部分的面积为△DEC面积的3倍,
∴得出结论则S3=6m.
理由:如图3,连接AD,BE,CF,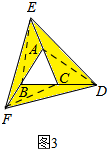
由(2)有,S△CDE=2m,
同(2)的方法得到,
S△EAF=2m,
S△BDF=2m,
∴S3=S△CDE+S△EAF+S△BDF=6m,
故答案为6m
(4)S△DEF=S阴影+S△ABC
=S3+S△ABC
=6m+m
=7m
=7S△ABC
∴得出结论扩展一次后得到的△DEF的面积是原来△ABC面积的7倍.
故答案为7.
(5)根据(4)结论可得两次扩展的区域(即阴影部分)面积共为(7×7-1)×15=720(平方米),
答:求这两次扩展的区域(即阴影部分)面积共为720平方米.
点评 本题考查了学生对面积公式的应用,同时考查到了学生的读题能力,利用类推的方法得出结论.解题的关键是找到扩展后的三角形的面积是原来的7倍.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
4.下列命题:①若a<1,则(a-1)$\sqrt{\frac{1}{1-a}}$=-$\sqrt{1-a}$;②平行四边形既是中心对称图形又是轴对称图形;③$\sqrt{9}$的算术平方根是3;④如果方程ax2+2x+1=0有两个不相等的实数根,则实数a<1.其中正确的命题个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.小雪在作业本上做了四道题目:①$\root{3}{-27}$=-3;②±$\sqrt{16}$=4;③$\root{3}{81}$=9;④$\sqrt{(-6)^{2}}$=6,她做对了的题目有( )
| A. | 1道 | B. | 2道 | C. | 3道 | D. | 4道 |
8.计算$\frac{1}{3}$-$\frac{1}{2}$的结果是( )
| A. | -$\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | -$\frac{5}{6}$ | D. | $\frac{5}{6}$ |
18.下列运算正确的是( )
| A. | (a2)5=a7 | B. | a2•a3=a5 | C. | (ab)2=a2b | D. | 3ab-2b=a |
5.下列几种组合中,恰不能密铺的是( )
| A. | 同样大小的任意四边形 | |
| B. | 边长相同的正三角形、正方形、正十二边形 | |
| C. | 边长相同的正十边形和正五角形 | |
| D. | 边长相同的正八边形和正三角形 |
14.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |