题目内容
4.下列命题:①若a<1,则(a-1)$\sqrt{\frac{1}{1-a}}$=-$\sqrt{1-a}$;②平行四边形既是中心对称图形又是轴对称图形;③$\sqrt{9}$的算术平方根是3;④如果方程ax2+2x+1=0有两个不相等的实数根,则实数a<1.其中正确的命题个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 分别根据平方根的定义、平行四边形的性质、一元二次方程根与判别式的关系对各小题进行逐一判断即可.
解答 解:①∵a<1,1-a>0,∴(a-1)$\sqrt{\frac{1}{1-a}}$=-$\sqrt{1-a}$,故本小题正确;
②平行四边形是中心对称图形但不是轴对称图形,故本小题错误;
③$\sqrt{9}$的算术平方根是$\sqrt{3}$,故本小题错误;
④∵方程ax2+2x+1=0有两个不相等的实数根,∴△=4-4a>0,解得a<1
又∵a≠0,
∴a<1且a≠0.故本小题错误.
故选A.
点评 本题考查的是命题与定理,熟知平方根的定义、平行四边形的性质、一元二次方程根与判别式的关系是解答此题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
14.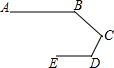 如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )
如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )
 如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )
如图是中国机器人创意设计大赛中一参赛队员设计的机器人比赛时行走的路径;机器人从A点出发,到达B点,第一次拐的∠B是140°,第二次拐的∠C是100°,第三次拐的角是∠D,这时机器人行走的路径恰好和出发时行走的路径平行,那么∠D的度数是( )| A. | 100° | B. | 120° | C. | 140° | D. | 90° |
15. 如图所示,直线a∥b,直线c与a、b相交,∠1=60°,则∠2等于( )
如图所示,直线a∥b,直线c与a、b相交,∠1=60°,则∠2等于( )
 如图所示,直线a∥b,直线c与a、b相交,∠1=60°,则∠2等于( )
如图所示,直线a∥b,直线c与a、b相交,∠1=60°,则∠2等于( )| A. | 60° | B. | 30° | C. | 120° | D. | 50° |
12.下列各长度的三条线段能组成三角形的是( )
| A. | 5、3、9 | B. | 5、3、8 | C. | 5、2、7 | D. | 5、3、6 |
19.下列式子从左到右的变形中是分解因式的为( )
| A. | y2-3y-4=y(y-3)-4 | B. | 1-4x+4x2=(1-2x)2 | C. | x2+y2=(x+y)(x-y) | D. | x-1=x(1-$\frac{1}{x}$) |
9. 如图是几何体的三视图,该几何体是( )
如图是几何体的三视图,该几何体是( )
 如图是几何体的三视图,该几何体是( )
如图是几何体的三视图,该几何体是( )| A. | 圆锥 | B. | 圆柱 | C. | 正三棱柱 | D. | 正三棱锥 |
16.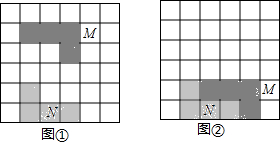 如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )
如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )
 如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )
如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )| A. | 向右平移2个单位,向下平移3个单位 | |
| B. | 向右平移1个单位,向下平移3个单位 | |
| C. | 向右平移1个单位,向下平移4个单位 | |
| D. | 向右平移2个单位,向下平移4个单位 |
5.设x是无理数,但(x-2)(x+6)是有理数,则下列式子中是有理数的是( )
| A. | x2 | B. | (x+6)2 | C. | (x+2)(x-6) | D. | (x+2)2 |