题目内容
14.定义:有一组邻边相等且对角线相等的四边形称为“美好四边形”.(1)从学过的特殊四边形中,写出一个“美好四边形”;
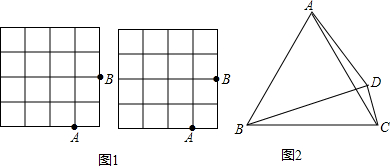
(2)如图,在4×4的网格图中有A、B两个格点,请在答题卷给出的两个网格图上各找出C、D两个格点,使得以A、B、C、D为顶点的四边形互不全等的“美好四边形”,画出相应的“美好四边形”,并写出该“美好四边形”的对角线长.
(3)如图,已知等边△ABC,在△ABC外存在点D,设∠BDC=α,∠DAC=β,探究α、β满足什么关系时,四边形ABCD为“美好四边形”.
分析 (1)根据正方形的性质和“美好四边形”的定义解答;
(2)根据“美好四边形”的定义作图,根据勾股定理求出对角线的长;
(3)根据等边三角形的性质和“美好四边形”的定义以及三角形内角和定理、等腰三角形的性质计算即可.
解答 解:(1)∵正方形四条边相等且对角线相等,满足“美好四边形”的条件,
∴正方形是“美好四边形”;
(2)图1中两个四边形ABCD都是“美好四边形”,
它们的对角线长都是$\sqrt{10}$;
(3)∵△ABC是等边三角形,四边形ABCD为“美好四边形”,
∴AB=AC=BC=BD,∠CBA=∠CAB=60°,
∵∠BDC=α,
∴∠BCD=α,
∴∠DBC=180°-2α,
∴∠ABD=60°-∠DBC=2α-120°,
∵BA=BD,
∴∠BAD=∠BDA=$\frac{180°-(2α-120°)}{2}$=150°-α,
∵∠DAC=β,
∴150°-α-β=60°,
∴α+β=90°.
点评 本题考查的是新定义、等腰三角形的性质、等边三角形的性质,正确理解“美好四边形”的定义、掌握等腰三角形的性质和等边三角形的性质是解题的关键.

练习册系列答案
相关题目
10.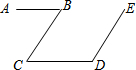 如图,AB∥CD,BC∥DE,若∠B=40°,则∠CDE的度数是( )
如图,AB∥CD,BC∥DE,若∠B=40°,则∠CDE的度数是( )
 如图,AB∥CD,BC∥DE,若∠B=40°,则∠CDE的度数是( )
如图,AB∥CD,BC∥DE,若∠B=40°,则∠CDE的度数是( )| A. | 40° | B. | 60° | C. | 140° | D. | 160° |
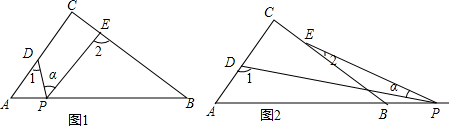
9. 如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )
如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )
 如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )
如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |

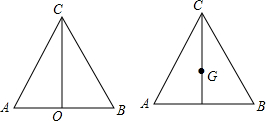
 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线与BE的延长线相交于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线与BE的延长线相交于点F,连接CF.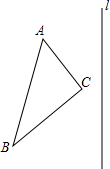 作图题,用直尺和圆规按下列要求作图.
作图题,用直尺和圆规按下列要求作图.