题目内容
6.在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出旋转后的点关于原点的对称点,这称为一次变换,已知点A的坐标为(-1,0),则点A经过连续2016次这样的变换得到的点A2016的坐标是(-1,0).分析 分别求得第一、二、三…八次变换后的坐标,得到每8次循环一次.则2016÷8=252即可求得结果.
解答 解:由题意第一次旋转后的坐标为($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),
第二次旋转后的坐标为(0,-1),
第三次旋转后的坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),
第四次旋转后的坐标为(1,0),
第五次旋转后的坐标为(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$),
第六次旋转后的坐标为(0,1),
第七次旋转后的坐标为($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),
第八次旋转后的坐标为(-1,0)
因为2016÷8=252,
所以把点A经过连续2016次这样的变换得到的点A2016的坐标是(-1,0).
故答案是:(-1,0).
点评 本题考查了坐标与图形变化-旋转.解答此类找规律的问题的关键是仔细分析题中所给的特征得到规律,再把这个规律应用于解题.

练习册系列答案
相关题目
2.化简$\sqrt{8}$的结果是( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
15.下列各数中,是方程x2=4x-3的解的是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |

 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).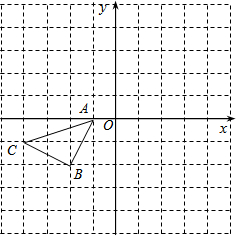 操作题
操作题 有一张地图,有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的南偏东45°,你能帮他确定C地的位置吗?
有一张地图,有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的南偏东45°,你能帮他确定C地的位置吗?