题目内容
9. 如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )
如图,已知AC⊥AB,∠1=30°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
分析 根据垂直定义可得∠BAC=90°,再根据角的和差关系可得∠2=∠BAC-∠1,进而可得答案.
解答 解:∵AC⊥AB,
∴∠BAC=90°,
∴∠1+∠2=90°,
∵∠1=30°,
∴∠2=60°,
故选:C.
点评 此题主要考查了垂线,关键是掌握垂线的定义当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
20.在实数$\frac{3}{2}$,0,-1,$\sqrt{3}$,最大的数是( )
| A. | $\frac{3}{2}$ | B. | 0 | C. | -1 | D. | $\sqrt{3}$ |
 如图,菱形ABCD的周长为20,对角线AC与BD相交于点O,AC=8,则BD=6.
如图,菱形ABCD的周长为20,对角线AC与BD相交于点O,AC=8,则BD=6.
 如图,在平面直角坐标系中,已知点A(0,8),点B(6,0),点P从B点以每秒1个单位的速度沿着BA方向出发,当点P运动到点A时停止,若设点P运动时间为t秒.
如图,在平面直角坐标系中,已知点A(0,8),点B(6,0),点P从B点以每秒1个单位的速度沿着BA方向出发,当点P运动到点A时停止,若设点P运动时间为t秒.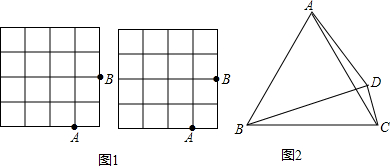
 如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2). 有一张地图,有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的南偏东45°,你能帮他确定C地的位置吗?
有一张地图,有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的南偏东45°,你能帮他确定C地的位置吗?