题目内容
14.等边三角形ABC的边长AB=10cm,则这个三角形的BC边上的高为( )cm.| A. | $\sqrt{50}$ | B. | $\sqrt{95}$ | C. | $\sqrt{15}$ | D. | $\sqrt{75}$ |
分析 过点A作AD⊥BC于点D,根据等边三角形的性质结合AB=10cm,即可得出BD=5cm,在Rt△ABD中,理由勾股定理即可求出AD的长度,此题得解.
解答 解:过点A作AD⊥BC于点D,如图所示.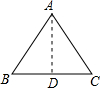
∵△ABC为等边三角形,AB=10cm,
∴BD=$\frac{1}{2}$BC=5cm.
在Rt△ABD中,AB=10cm,BD=5cm,∠ADB=90°,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{75}$=5$\sqrt{3}$cm.
故选D.
点评 本题考查了等边三角形的性质以及解直角三角形,根据等边三角形的性质结合勾股定理求出AD的长度是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
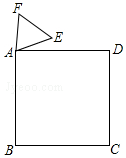 如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小是15°或165°.
如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小是15°或165°. 如图,直线AB、CD相交于点O,∠1-∠2等于50°,则∠2=115°,∠BOD=65°.
如图,直线AB、CD相交于点O,∠1-∠2等于50°,则∠2=115°,∠BOD=65°.