题目内容
14.已知ab≠0,方程ax2+bx+c=0的系数满足($\frac{b}{2}$)2=ac,则方程的两根之比为( )| A. | 0:1 | B. | 1:1 | C. | 1:2 | D. | 2:3 |
分析 首先整理($\frac{b}{2}$)2=ac,得出b2-4ac=0,判断方程有两个相等的实数根,由此得出两个根的比即可.
解答 解:∵ab≠0,方程ax2+bx+c=0的系数满足($\frac{b}{2}$)2=ac,
∴b2-4ac=0,
∴方程有两个相等的实数根,则方程的两根之比为1:1.
故选:B.
点评 此题考查了根的判别式;一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
9.方程组$\left\{\begin{array}{l}{2x-y=3}\\{x+3y=5}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ |
4.已知a<b,下列不等式中,变形正确的是( )
| A. | a-3>b-3 | B. | $\frac{a}{3}>\frac{b}{3}$ | C. | -3a>-3b | D. | 3a-1>3b-1 |
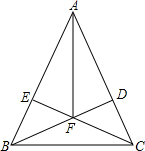 如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.试说明AF平分∠BAC的理由.
如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.试说明AF平分∠BAC的理由.
 如图,在每个小正方形边长都为1的正方形网格中,经过格点A、B、C的弧所在圆的面积为$\frac{37}{2}π$.(结果保留准确值)
如图,在每个小正方形边长都为1的正方形网格中,经过格点A、B、C的弧所在圆的面积为$\frac{37}{2}π$.(结果保留准确值)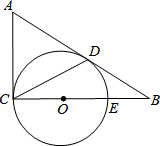 如图,在△ABC中,∠ACB=90°,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=3.
如图,在△ABC中,∠ACB=90°,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=3.