题目内容
16.计算:$\sqrt{16}$+$\root{3}{-64}$-$\sqrt{(-3)^{2}}$+|$\sqrt{3}$-1|.分析 根据实数的运算顺序,首先计算乘方、开方,然后从左向右依次计算,求出算式$\sqrt{16}$+$\root{3}{-64}$-$\sqrt{(-3)^{2}}$+|$\sqrt{3}$-1|的值是多少即可.
解答 解:$\sqrt{16}$+$\root{3}{-64}$-$\sqrt{(-3)^{2}}$+|$\sqrt{3}$-1|
=4-4-3$+\sqrt{3}-1$
=$\sqrt{3}-4$.
点评 此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到有的顺序进行.另外,有理数的运算律在实数范围内仍然适用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
7.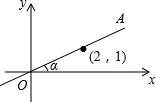 如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
 如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
4.已知a<b,下列不等式中,变形正确的是( )
| A. | a-3>b-3 | B. | $\frac{a}{3}>\frac{b}{3}$ | C. | -3a>-3b | D. | 3a-1>3b-1 |
6.一个图形无论经过平移还是旋转,有以下说法:
(1)对应线段平行;
(2)对应线段相等;
(3)对应角相等;
(4)不改变图形的形状和大小,
其中正确的有( )
(1)对应线段平行;
(2)对应线段相等;
(3)对应角相等;
(4)不改变图形的形状和大小,
其中正确的有( )
| A. | (1)(2)(3) | B. | (1)(2)(4) | C. | (1)(3)(4) | D. | (2)( 3)(4) |
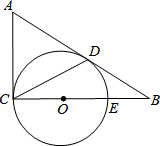 如图,在△ABC中,∠ACB=90°,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=3.
如图,在△ABC中,∠ACB=90°,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=3. 如图,将一个三角板的直角顶点放在直尺的一条边上,若∠1=50°,则∠2的度数为40°.
如图,将一个三角板的直角顶点放在直尺的一条边上,若∠1=50°,则∠2的度数为40°.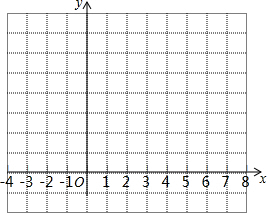 已知△ABC的三个顶点的坐标分别是A(0,1),B(2,0),C(2,3).
已知△ABC的三个顶点的坐标分别是A(0,1),B(2,0),C(2,3). 如图,直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b的解集为x<-1.
如图,直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b的解集为x<-1.