题目内容
16. 第1个正方形A1B1C1O,第2个正方形A2B2C2C1,第3个正方形A3B3C3C2,…按如图所示方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则第n个正方形的边长为( )
第1个正方形A1B1C1O,第2个正方形A2B2C2C1,第3个正方形A3B3C3C2,…按如图所示方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则第n个正方形的边长为( )| A. | n | B. | 2n-1 | C. | 2n-1 | D. | 2n-1 |
分析 首先求得直线的解析式,分别求得经过正方形的边长,可以得到一定的规律,据此即可求解.
解答 解:∵正方形A1B1C1O,点B1(1,1),B2(3,2),
∴A1的坐标是(0,1),A2的坐标是:(1,2),
∵点A1,A2,A3,…在直线y=kx+b(k>0)上,
∴$\left\{\begin{array}{l}{b=1}\\{k+b=2}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴直线的解析式是:y=x+1,
∵C2的横坐标是3,A3的纵坐标为4,
∴第1个正方形A1B1C1O的边长为1,第2个正方形A2B2C2C1边长为2,第3个正方形A3B3C3C2边长为4,
第4个正方形的边长为8,…
第n个正方形的边长为2n-1.
故选D.
点评 本题主要考查了坐标的变化规律,由待定系数法求函数解析式,正确得到点的坐标的规律是解题的关键.

练习册系列答案
相关题目
11.若方程组$\left\{\begin{array}{l}3x+y=1+3a\\ x+3y=1-a\end{array}\right.$的解满足x-y=-2,则a的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 不能确定 |
1.台州市2012年5月的平均房价为9530元/m2,2014年同期达到11284元/m2,假设这两年台州市房价的平均增长率为x,根据题意,则下列所得的方程中,正确的是( )
| A. | 9530(1+x%)2=11284 | B. | 9530(1-x%)2=11284 | C. | 9530(1+x)2=11284 | D. | 9530(1-x)2=11284 |
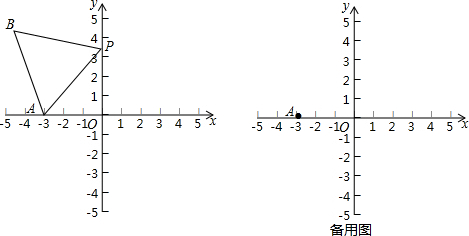
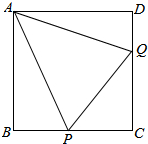 如图所示,在正方形ABCD中,P,Q分别在边BC,CD上,PB+QD=PQ,求证:∠PAQ=45°.
如图所示,在正方形ABCD中,P,Q分别在边BC,CD上,PB+QD=PQ,求证:∠PAQ=45°.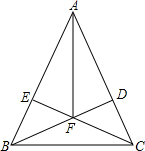 如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.试说明AF平分∠BAC的理由.
如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.试说明AF平分∠BAC的理由.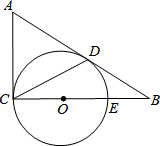 如图,在△ABC中,∠ACB=90°,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=3.
如图,在△ABC中,∠ACB=90°,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=3.