题目内容
1.解方程:(1)$\frac{6}{{{x^2}-9}}$+$\frac{x}{x-3}$=1;
(2)(x-2)2=2x-4.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)方程整理后,利用因式分解法求出解即可.
解答 解:(1)去分母得:6+x(x+3)=x2-9,
解得:x=-5,
经检验x=-5是原方程的根;
(2)方程整理得:(x-2)2-2(x-2)=0,
分解因式得:(x-2)(x-4)=0,
解得:x1=2,x2=4.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
11.若方程组$\left\{\begin{array}{l}3x+y=1+3a\\ x+3y=1-a\end{array}\right.$的解满足x-y=-2,则a的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 不能确定 |
9.方程组$\left\{\begin{array}{l}{2x-y=3}\\{x+3y=5}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ |
13.下列运算正确的是( )
| A. | (3xy2)2=6xy4 | B. | 2x-2=$\frac{1}{2{x}^{2}}$ | C. | x7÷x5=x2 | D. | (a+1)2=a2+1 |
10.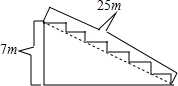 如图,某公司举行周年庆典,准备在门口长25米,高7米的台阶上铺设红地毯,已知台阶的宽为3米,则共需购买( )m2的红地毯.
如图,某公司举行周年庆典,准备在门口长25米,高7米的台阶上铺设红地毯,已知台阶的宽为3米,则共需购买( )m2的红地毯.
 如图,某公司举行周年庆典,准备在门口长25米,高7米的台阶上铺设红地毯,已知台阶的宽为3米,则共需购买( )m2的红地毯.
如图,某公司举行周年庆典,准备在门口长25米,高7米的台阶上铺设红地毯,已知台阶的宽为3米,则共需购买( )m2的红地毯.| A. | 21 | B. | 75 | C. | 93 | D. | 96 |
 如图,AB,CD相交于点O,AC∥DB,E,F为AB上的两点,且AE=BF,OC=OD,求证:CE=DF.
如图,AB,CD相交于点O,AC∥DB,E,F为AB上的两点,且AE=BF,OC=OD,求证:CE=DF.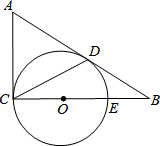 如图,在△ABC中,∠ACB=90°,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=3.
如图,在△ABC中,∠ACB=90°,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=3. 如图,将一个三角板的直角顶点放在直尺的一条边上,若∠1=50°,则∠2的度数为40°.
如图,将一个三角板的直角顶点放在直尺的一条边上,若∠1=50°,则∠2的度数为40°.