题目内容
17.已知△ABC是等边三角形,BC=2cm,点D是直线BC上的一动点,以AD为边在直线BC的同侧作等边△ADE.过点C作CF∥DE交直线AB于点F,连接EF.(1)如图1,当点D在线段BC上时,求证:四边形DCFE是平行四边形;
(2)如图2,点D从B点出发,在直线BC上沿B点左侧以每秒1cm的速度移动,移动时间为t秒(t>0).
①当t=2时,求证:四边形DCFE是矩形;
②在点D的移动过程中,四边形DCFE有没有可能成为菱形?说明理由.
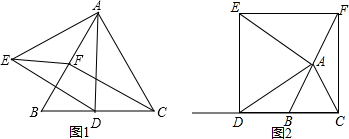
分析 (1)根据△ABC和△AED是等边三角形,D是BC的中点,ED∥CF,求证△ABD≌△CAF,进而求证四边形EDCF是平行四边形即可;
(2)①根据△ABC和△AED是等边三角形,D是BC的中点,ED∥CF,求证△ABD≌△CAF,进而求证四边形EDCF是平行四边形,再得出∠EDC=90°,证明矩形即可;
②根据分析得出DC>ED,故不能为菱形.
解答 解:(1)∵△ABC和△ADE是等边三角形,
∴∠ABC=∠ADE=∠CAB=60°,AB=CA,
∴∠BDA=∠ADE+∠BDE=60°+∠BDE,
∠AFC=∠ABC+∠BCF=60°+∠BCF,
∵CF∥DE,
∴∠BDE=∠BCF,
∴∠BDA=∠AFC,
在△BAD和△ACF中
$\left\{\begin{array}{l}{∠ABD=∠CAF}\\{∠BDA=∠AFC}\\{AB=CA}\end{array}\right.$,
∴△BAD≌△ACF(AAS),
∴AD=CF,
∵AD=DE,
∴DE$\stackrel{∥}{=}$CF,
∴四边形DCFE是平行四边形;
(2)①∵△ABC和△ADE是等边三角形,
∴∠ABC=∠ADE=∠BAC=60°,AB=CA,
∴∠BDA=180°-∠ADE-∠GDE=120°-∠GDE,
∠AFC=180°-∠ABC-∠BCF=120°-∠BCF,
∵CF∥DE,
∴∠GDE=∠BCF,
∴∠BDA=∠AFC,
在△BAD和△ACF中,
$\left\{\begin{array}{l}{∠ABD=∠CAF=120°}\\{∠BDA=∠AFC}\\{AB=CA}\end{array}\right.$,
∴△BAD≌△ACF(AAS),
∴AD=CF,
∵AD=DE,
∴DE$\stackrel{∥}{=}$CF,
∴四边形DCFE是平行四边形,
∵DB=AB=2,∠ADB+∠BAD=∠ABC=60°,
∴∠ADB=∠BAD=30°,
∴∠EDC=∠ADE+∠ADB=90°,
∴平行四边形DCFE是矩形;
②四边形DCFE不可能成为菱形,
∵t>0,
∴BD>0
在△BAD中,AB+BD>AD,
∵△ABC和△ADE是等边三角形,
∴AD=DE,AB=BC,
∴BC+BD>DE,即DC>ED,
∴四边形DCFE不可能成为菱形.
点评 此题主要考查学生对平行四边形的判定和性质、全等三角形的判定和性质、等边三角形的性质的理解和掌握.此题涉及到的知识点较多,综合性较强,难度较大.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ |
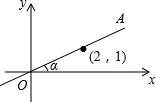 如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
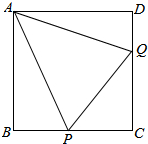 如图所示,在正方形ABCD中,P,Q分别在边BC,CD上,PB+QD=PQ,求证:∠PAQ=45°.
如图所示,在正方形ABCD中,P,Q分别在边BC,CD上,PB+QD=PQ,求证:∠PAQ=45°. 如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.试说明AF平分∠BAC的理由.
如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.试说明AF平分∠BAC的理由.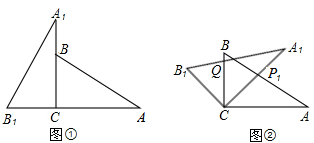

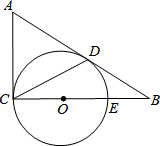 如图,在△ABC中,∠ACB=90°,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=3.
如图,在△ABC中,∠ACB=90°,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=3.