题目内容
12.计算题(1)-5+(+21)-(-79)-15
(2)2(m-3n)-(-3m-2n)
(3)-($\frac{5}{9}$-$\frac{3}{4}$+$\frac{1}{18}$)÷$\frac{1}{36}$
(4)-$\frac{2}{3}$÷[-32×(-$\frac{2}{3}$)2+2]×(-1)2013.
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式去括号合并即可得到结果;
(3)原式利用除法法则变形,再利用乘法分配律计算即可得到结果;
(4)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解答 解:(1)原式=-5+21+79-15=-20+100=80;
(2)原式2m-6n+3m+2n=5m-4n;
(3)原式=-($\frac{5}{9}$-$\frac{3}{4}$+$\frac{1}{18}$)×36=-20+27-2=5;
(4)原式=-$\frac{2}{3}$÷(-9×$\frac{4}{9}$+2)×(-1)=-$\frac{2}{3}$÷(-4+2)×(-1)=-$\frac{2}{3}$×(-$\frac{1}{2}$)×(-1)=-$\frac{1}{3}$.
点评 此题考查了有理数的混合运算,以及整式的加减,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.下列根式中,是最简根式的是( )
| A. | $\sqrt{\frac{{a}^{3}b}{5}}$ | B. | $\sqrt{{a}^{3}{b}^{2}-a{b}^{2}}$ | C. | $\frac{\sqrt{{a}^{2}+{b}^{2}}}{2}$ | D. | $\sqrt{{a}^{2}-2ab+{b}^{2}}$ |
3.对下列各整式因式分解正确的是( )
| A. | 2x2-x+1=x(2x-1)+1 | B. | x2-2x-1=(x2-1)2 | ||
| C. | 2x2-xy-x=2x(x-y-1) | D. | x2-x-6=(x+2)(x-3) |
1.如图,从边长为a+2的正方形纸片中剪去一个边长为a-1的正方形(a>1),剩余部分沿虚线剪开,再拼成一个长方形(不重叠无缝隙),则该长方形的面积是( )
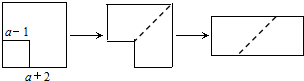

| A. | 4a+1 | B. | 4a+3 | C. | 6a+3 | D. | a2+1 |
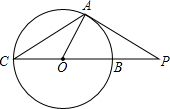 如图,已知CB是⊙O的直径,点A在圆上,且∠AOB=60°,连接OA,过点A作PA⊥OA交CB的延长线于点P,PA=4$\sqrt{3}$.
如图,已知CB是⊙O的直径,点A在圆上,且∠AOB=60°,连接OA,过点A作PA⊥OA交CB的延长线于点P,PA=4$\sqrt{3}$.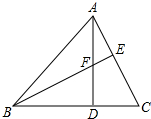 如图,已知AD是△ABC的高,F是AD上一点,BF的延长线交AC于点E,BF=AC,DF=DC,则BF与AC垂直吗?为什么?
如图,已知AD是△ABC的高,F是AD上一点,BF的延长线交AC于点E,BF=AC,DF=DC,则BF与AC垂直吗?为什么? 已知:如图,∠ACB=∠ADB=90°,AD=AC,E是AB上一点,判断图中有几对相等的角,并证明你的结论.
已知:如图,∠ACB=∠ADB=90°,AD=AC,E是AB上一点,判断图中有几对相等的角,并证明你的结论.