题目内容
20.二次函数y=x2+bx+c的图象经过点(4,3),(3,0),求函数y的表达式,并求出当0≤x≤3时,y的最大值.分析 利用待定系数法求出二次函数的解析式,根据二次函数的性质求出最大值即可.
解答 解:∵二次函数y=x2+bx+c的图象经过点(4,3),(3,0),
∴$\left\{\begin{array}{l}{16+4b+c=3}\\{9+3b+c=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{b=-4}\\{c=3}\end{array}\right.$,
∴函数解析式为:y=x2-4x+3,
y=x2-4x+3=(x-2)2-1,
∴当x=0时,y有最大值是3.
点评 本题考查的是待定系数法求二次函数的解析式和二次函数的最值,掌握待定系数法求解析式的一般步骤是解题的关键.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
11.分解因式(2x+3)2-x2的结果是( )
| A. | 3(x2+4x+3) | B. | 3(x2+2x+3) | C. | (3x+3)(x+3) | D. | 3(x+1)(x+3) |
5.化简$\frac{{x}^{2}}{x-2}+\frac{4}{2-x}$的结果是( )
| A. | x-2 | B. | $\frac{1}{x-2}$ | C. | $\frac{{x}^{2}+4}{x-2}$ | D. | x+2 |
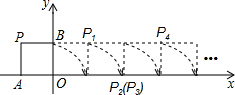 如图,将边长为1的正方形OPAB沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…,P2014,P2015的位置,记Pi(xi,yi),i=1,2,3,…,2014,2015,则P2015的横坐标为2014.
如图,将边长为1的正方形OPAB沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…,P2014,P2015的位置,记Pi(xi,yi),i=1,2,3,…,2014,2015,则P2015的横坐标为2014.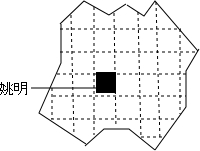 某包装公司想用一张不规则的包装纸做一个正方体纸盒,如图.
某包装公司想用一张不规则的包装纸做一个正方体纸盒,如图.