题目内容
4.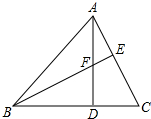 如图,已知AD是△ABC的高,F是AD上一点,BF的延长线交AC于点E,BF=AC,DF=DC,则BF与AC垂直吗?为什么?
如图,已知AD是△ABC的高,F是AD上一点,BF的延长线交AC于点E,BF=AC,DF=DC,则BF与AC垂直吗?为什么?
分析 由AD是△ABC的高,于是得到∠ADB=∠ADC=90°,推出Rt△ADC≌Rt△BDF,根据全等三角形的性质得到∠FBD=∠CAD,由于∠CAD+∠C=90°,于是得到∠DBF+∠C=90°,即可得到结论.
解答 解:BF与AC垂直,
理由:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°,
在Rt△ADC与Rt△BDF中,
$\left\{\begin{array}{l}{AC=BF}\\{CD=DF}\end{array}\right.$,
∴Rt△ADC≌Rt△BDF,
∴∠FBD=∠CAD,
∵∠CAD+∠C=90°,
∴∠DBF+∠C=90°,
∴∠BEC=90°,
∴BF⊥AC.
点评 本题考查了全等三角形的判定与性质、垂线的判定;熟练掌握全等三角形的判定方法,证明三角形全等得出对应角相等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.在直角坐标系xOy中,已知P(m,n),m、n满足(m2+1+n2)(m2+4+n2)=10,则OP的长( )
| A. | $\sqrt{6}$ | B. | 6 | C. | $\sqrt{6}$或1 | D. | 1 |
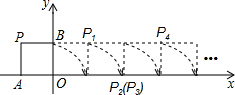 如图,将边长为1的正方形OPAB沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…,P2014,P2015的位置,记Pi(xi,yi),i=1,2,3,…,2014,2015,则P2015的横坐标为2014.
如图,将边长为1的正方形OPAB沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…,P2014,P2015的位置,记Pi(xi,yi),i=1,2,3,…,2014,2015,则P2015的横坐标为2014.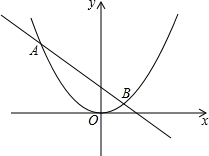 已知抛物线y=$\frac{1}{4}$x2与直线y=$-\frac{3}{4}$x+1交于A、B两点(A在B的左侧)
已知抛物线y=$\frac{1}{4}$x2与直线y=$-\frac{3}{4}$x+1交于A、B两点(A在B的左侧)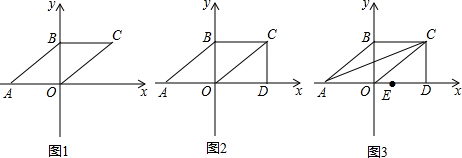
 如图,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB的中点,连结CE、CD,求证:
如图,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB的中点,连结CE、CD,求证: