题目内容
17.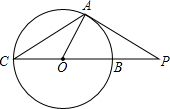 如图,已知CB是⊙O的直径,点A在圆上,且∠AOB=60°,连接OA,过点A作PA⊥OA交CB的延长线于点P,PA=4$\sqrt{3}$.
如图,已知CB是⊙O的直径,点A在圆上,且∠AOB=60°,连接OA,过点A作PA⊥OA交CB的延长线于点P,PA=4$\sqrt{3}$.(1)求⊙O的半径;
(2)求△AOC的面积.
分析 (1)设OA为x,根据直角三角形的性质用x表示出OP,根据勾股定理列出方程,解方程即可;
(2)根据等高的两个三角形的面积比等于对应的底的比解答即可.
解答 解:(1)∵PA⊥OA,∠A0B=60°,
∴∠APO=30°,
∴OA=$\frac{1}{2}$OP,
设OA为x,则OP为2x,
在Rt△OAP中,OA2+PA2=OP2,即x2+(4$\sqrt{3}$)2=(2x)2,
解得,x=4,
∴圆的半径为4;
(2)∵OA=4,
∴△AOP的面积为$\frac{1}{2}$×OA×AP=8$\sqrt{3}$,
∵OP=8,OC=4,
∴△AOC的面积=$\frac{1}{2}$×△AOP的面积=4$\sqrt{3}$.
点评 本题考查的是直角三角形的性质、圆心角定理和勾股定理的应用,掌握等高的两个三角形的面积比等于对应的底的比是解题的关键.

练习册系列答案
相关题目
5.化简$\frac{{x}^{2}}{x-2}+\frac{4}{2-x}$的结果是( )
| A. | x-2 | B. | $\frac{1}{x-2}$ | C. | $\frac{{x}^{2}+4}{x-2}$ | D. | x+2 |
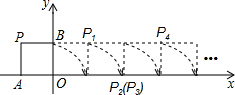 如图,将边长为1的正方形OPAB沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…,P2014,P2015的位置,记Pi(xi,yi),i=1,2,3,…,2014,2015,则P2015的横坐标为2014.
如图,将边长为1的正方形OPAB沿x轴正方向连续翻转2015次,点P依次落在点P1,P2,P3,…,P2014,P2015的位置,记Pi(xi,yi),i=1,2,3,…,2014,2015,则P2015的横坐标为2014. 如图,D为△ABC的边BC的中点,F为AC边上的点,AF=$\frac{1}{2}$FC,BF交AD于点E.求证:点E为AD的中点.
如图,D为△ABC的边BC的中点,F为AC边上的点,AF=$\frac{1}{2}$FC,BF交AD于点E.求证:点E为AD的中点.