题目内容

1．如图，从边长为a+2的正方形纸片中剪去一个边长为a-1的正方形（a＞1），剩余部分沿虚线剪开，再拼成一个长方形（不重叠无缝隙），则该长方形的面积是（　　）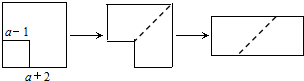
A．4a+1B．4a+3C．6a+3D．a2+1

分析 依据长方形的面积等于大正方形的面积-小正方形的面积求解即可．

解答 解：长方形的面积=（a+2）2-（a-1）2
=a2+4a+4-a2+2a-1
=6a+3．
故选：C．

点评 本题主要考查的是图形的剪拼，明确长方形的面积等于大正方形的面积-小正方形的面积是解题的关键．

练习册系列答案
相关题目
11．分解因式（2x+3）2-x2的结果是（　　）
A．3（x2+4x+3）B．3（x2+2x+3）C．（3x+3）（x+3）D．3（x+1）（x+3）
12．计算题
（1）-5+（+21）-（-79）-15
（2）2（m-3n）-（-3m-2n）
（3）-（$\frac{5}{9}$-$\frac{3}{4}$+$\frac{1}{18}$）÷$\frac{1}{36}$              
（4）-$\frac{2}{3}$÷[-32×（-$\frac{2}{3}$）2+2]×（-1）2013．
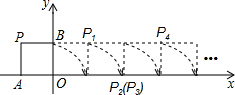9．如图，将边长为1的正方形OPAB沿x轴正方向连续翻转2015次，点P依次落在点P1，P2，P3，…，P2014，P2015的位置，记Pi（xi，yi），i=1，2，3，…，2014，2015，则P2015的横坐标为2014．
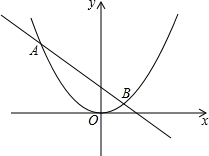16．已知抛物线y=$\frac{1}{4}$x2与直线y=$-\frac{3}{4}$x+1交于A、B两点（A在B的左侧）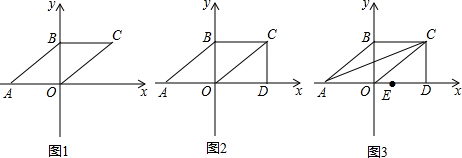
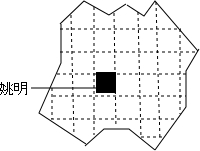（1）求A、B两点的坐标．
（2）在直线AB的下方的抛物线上有一点D，使得ABD面积最大，求点D的坐标．
（3）把抛物线向右平移2个单位，再向下平移m（m＞0）个单位，平移后的抛物线与x轴交于E、F两点，直线AB与y轴交于点C．当m为何值时，过E、F、C三点的圆的面积最小，最小面积是多少？
6．在研究问题“已知$\left\{\begin{array}{l}{3a+7b+c=4}\\{a-b-3c=8}\end{array}\right.$，求a+b-c的值．”时，三个同学各提出了自己的看法．甲说：“三个未知数，两个方程，条件不够，不能求出abc的值，a+b-c的值很难确定．”；乙说：“是求a+b-c的值，可以把a+b-c看做一个整体，设a+b-c=m，应该可以求解”；丙说：“可以把其中一个未知数c当做已知量，三元一次方程组化为二元一次方程组，从而求出a，b的表达式，再求a+b-c的值”．
（1）根据他们的说法，请用合适的方法求a+b-c的值；
（2）若已知b≤c，你能确定c2+a-2b是否有最值？若有，请求出最值和相应的a、b、c的值．
13．如图1：在平面直角坐标系内，O为坐标原点，线段AB两端点在坐标轴上且点A（-4，0）点B（0，3），将AB向右平移4个单位长度至OC的位置
（1）直接写出点C的坐标（4，3）；
（2）如图2，过点C作CD⊥x轴于点D，在x轴正半轴有一点E（1，0），过点E作x轴的垂线，在垂线上有一动点P，求三角形PCD的面积；
（3）如图3，在（2）的条件下，连接AC，当△ACP的面积为$\frac{33}{2}$时，求点P的坐标．
3．某包装公司想用一张不规则的包装纸做一个正方体纸盒，如图．
（1）包装纸上恰好有NBA球星姚明、易建联贴图各一张，包装公司想用这两张贴图分别作纸盒的两个面，请你帮助公司设计剪裁方案（在图中用实线框出需要剪下的方格）；
（2）公司想在姚明头像相对的一面写上“姚”字，根据你刚才的剪法，在相应的位置写上“姚”字（在图中写）．
4．先化简，再求值．
（1）[（x-y）2+（x+y）（x-y）]÷2x，其中x=3，y=-1.5
（2）$\frac{{x}^{2}-1}{x-1}$+x（1+$\frac{1}{x}$），其中x=-$\frac{1}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网