题目内容
2.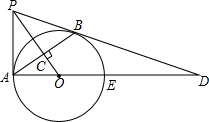 如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.(1)求证:PA是⊙O的切线;
(2)若AC=6,OC=4,求PA的长.
分析 (1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;
(2)连接BE,由AC=6,OC=4,可求OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.
解答 (1)证明:连接OB,则OA=OB,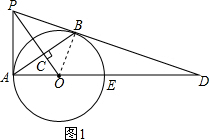
∵OP⊥AB,
∴AC=BC,
∴OP是AB的垂直平分线,
∴PA=PB,
在△PAO和△PBO中,
∵$\left\{\begin{array}{l}{PA=PB}\\{OP=PO}\\{OA=OB}\end{array}\right.$,
∴△PAO≌△PBO(SSS)
∴∠PBO=∠PAO,PB=PA,
∵PB为⊙O的切线,B为切点,
∴∠PBO=90°,
∴∠PAO=90°,
即PA⊥OA,
∴PA是⊙O的切线;
(2)解:连接BE,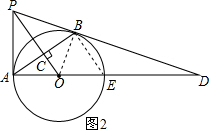
∵OC=4,AC=6,
∴AB=12,
在Rt△ACO中,
由勾股定理得:AO=$\sqrt{A{C}^{2}+O{C}^{2}}$=2$\sqrt{13}$,
∴AE=2OA=4$\sqrt{13}$,OB=OA=2$\sqrt{13}$,
在Rt△APO中,
∵AC⊥OP,
∴AC2=OC•PC,
解得:PC=9,
∴OP=PC+OC=13,
在Rt△APO中,由勾股定理得:AP=$\sqrt{O{P}^{2}-O{A}^{2}}$=3$\sqrt{13}$,
点评 本题考查了全等三角形的判断和性质,切线的性质和判定,做好本题是明确两点:①圆的切线垂直于经过切点的半径. ②经过半径的外端且垂直于这条半径的直线是圆的切线.

练习册系列答案
相关题目
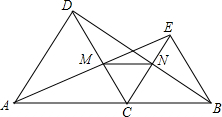 如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.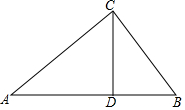 某景区把一块三角形的废地开辟为动物园,如图所示,测得AC=80m,BC=60m,AB=100m.
某景区把一块三角形的废地开辟为动物园,如图所示,测得AC=80m,BC=60m,AB=100m.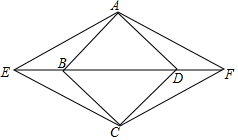 已知:如图,在菱形ABCD中,E、F分别在射线DB和射线BD上,且BE=DF.
已知:如图,在菱形ABCD中,E、F分别在射线DB和射线BD上,且BE=DF.