题目内容
12.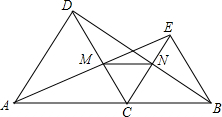 如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.(1)求证:AE=BD;
(2)求证:MN∥AB.
(3)设AE和DB的交点为F,连FC,求证:FC平分∠AFB.
分析 (1)先由△ACD和△BCE是等边三角形,可知AC=DC,CE=CB,∠DCA=60°,∠ECB=60°,故可得出∠DCA+∠DCE=∠ECB+∠DCE,∠ACE=∠DCB,根据SAS定理可知△ACE≌△DCB,由全等三角形的性质即可得出结论;
(2)由(1)中△ACE≌△DCB,可知∠CAM=∠CDN,再根据∠ACD=∠ECB=60°,A、C、B三点共线可得出∠DCN=60°,由全等三角形的判定定理可知,△ACM≌△DCN,故MC=NC,再根据∠MCN=60°可知△MCN为等边三角形,故∠NMC=∠DCN=60°故可得出结论.
(3)作CP⊥AE,CQ⊥DB,由△ACE≌△DCB可得它们的面积相等,即可得到CP=CQ,再由角平分线的逆定理可得FC平分∠AFB.
解答 证明:(1)∵△ACD和△BCE是等边三角形,
∴AC=DC,CE=CB,∠DCA=60°,∠ECB=60°,
∵∠DCA=∠ECB=60°,
∴∠DCA+∠DCE=∠ECB+∠DCE,∠ACE=∠DCB,
在△ACE与△DCB中,
∵$\left\{\begin{array}{l}{AC=DC}\\{∠ACE=∠DCB}\\{CE=CB}\end{array}\right.$,
∴△ACE≌△DCB,
∴AE=BD;
(2)∵由(1)得,△ACE≌△DCB,
∴∠CAM=∠CDN,
∵∠ACD=∠ECB=60°,而A、C、B三点共线,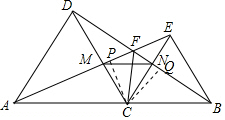
∴∠DCN=60°,
在△ACM与△DCN中,
∵$\left\{\begin{array}{l}{∠MAC=∠NDC}\\{AC=DC}\\{∠ACM=∠DCN}\end{array}\right.$,
∴△ACM≌△DCN(ASA),
∴MC=NC,
∵∠MCN=60°,
∴△MCN为等边三角形,
∴∠NMC=∠DCN=60°,
∴∠NMC=∠DCA,
∴MN∥AB.
(3)作CP⊥AE,CQ⊥DB,
∵△ACE≌△DCB,
∴S△ACE=S△DCB,
∴$\frac{1}{2}$AE•PC=$\frac{1}{2}$BD•CQ,
∴PC=CQ,
∵CP⊥AE,CQ⊥DB,
∴∠AFC=∠BFC,
∴FC平分∠AFB.
点评 本题考查的是等边三角形的判定与性质及全等三角形的判定与性质,根据题意判断出△ACE≌△DCB,△ACM≌△DCN是解答此题的关键.

| A. | (1,-2) | B. | (-1,2) | C. | (-1,-2) | D. | (1,2) |
①$\sqrt{15}$;②$\sqrt{\frac{1}{a}}$;③$\sqrt{{a}^{2}+{b}^{2}}$;④$\sqrt{{a}^{2}b}$;⑤$\sqrt{2ab×3bc}$;⑥$\sqrt{5\frac{1}{2}}$.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | (ab)4÷(ab3)=ab | B. | a10÷(a5÷a3)=a8 | C. | xm+3÷xm+1=x3 | D. | (x3n÷xn)÷x2n=x |
 如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.求证:AM=DM.
如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.求证:AM=DM.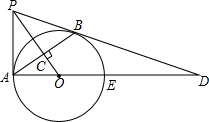 如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.