题目内容
12.在菱形ABCD中,∠A=60°,AB=4$\sqrt{3}$,点P在菱形内,若PB=PD=4,则∠PDC的度数为90°或30°.分析 分成P在OA上和P在OC上两种情况进行讨论,根据△ABD是等边三角形可得BD=AB=4$\sqrt{3}$,OB=OD=$\frac{1}{2}$BD=2$\sqrt{3}$,∠ADO=60°,再利用三角函数值可得∠PDO=30°,进而可得答案.
解答 解: 设AC和BE相交于点O.
设AC和BE相交于点O.
当P在OA上时,
∵AB=AD,∠A=60°,
∴△ABD是等边三角形,
∴BD=AB=4$\sqrt{3}$,OB=OD=$\frac{1}{2}$BD=2$\sqrt{3}$,∠ADO=60°,
∴cos∠PDO=$\frac{DO}{PD}$=$\frac{\sqrt{3}}{2}$,
∴∠PDO=30°,
∴∠ADP=60°-30°=30°,
∵四边形ABCD是菱形,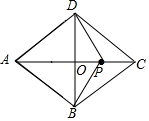
∴AB∥CD,
∴∠ADC=180°-60°=120°,
∴∠PDC=120°-30°=90°,
当P在OC上时,∵四边形ABCD是菱形,
∴∠DCB=∠DAB=60°,DC=BC,
∴△DBC是等边三角形,
∴∠BDC=60°,
∵∠PDO=30°,
∴∠PDC=30°,
故答案为:90°或30°.
点评 本题考查了菱形的性质,注意到P在AC上,应分两种情况进行讨论是解题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
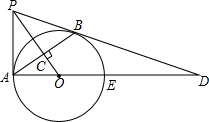 如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.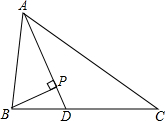 如图,△ABC中,AD平分∠BAC,BP⊥AD于点P,AB=5,BP=1,AC=9,说明∠ABP=2∠ACB的理由.
如图,△ABC中,AD平分∠BAC,BP⊥AD于点P,AB=5,BP=1,AC=9,说明∠ABP=2∠ACB的理由.