题目内容
7.(1)$\sqrt{12}$+$\sqrt{27}$+$\frac{1}{4}$$\sqrt{48}$-15$\sqrt{\frac{1}{3}}$(2)(2$\sqrt{3}$+$\sqrt{5}$)2-(2$\sqrt{3}$-$\sqrt{5}$)2
(3)$\left\{\begin{array}{l}{2a+3b=2}\\{4a-9b=-1}\end{array}\right.$
(4)$\left\{\begin{array}{l}{3x+2y=21}\\{2x-y=14}\end{array}\right.$.
分析 (1)先把各二次根式化简为最简二次根式,然后合并即可;
(2)利用完全平方公式展开,然后合并即可;
(3)、(4)利用加减消元法解方程组.
解答 解:(1)原式=2$\sqrt{3}$+3$\sqrt{3}$+$\sqrt{3}$-5$\sqrt{3}$
=$\sqrt{3}$;
(2)原式=12+4$\sqrt{15}$+5-(12-4$\sqrt{15}$+5)
=8$\sqrt{15}$;
(3)$\left\{\begin{array}{l}{2a+3b=2①}\\{4a-9b=-1②}\end{array}\right.$,
①×3+②得10a=5,解得a=$\frac{1}{2}$,
①×2-②得15b=5,解得b=$\frac{1}{3}$,
所以方程组的解为$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=\frac{1}{3}}\end{array}\right.$;
(4)$\left\{\begin{array}{l}{3x+2y=21①}\\{2x-y=14①}\end{array}\right.$,
①+②×2得7x=49,解得x=7,
把x=7代入②得14-y=14,解得y=0,
所以方程组的解为$\left\{\begin{array}{l}{x=7}\\{y=0}\end{array}\right.$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了解二元一次方程组.

练习册系列答案
相关题目
18.某商厦服装柜在销售中发现某品牌的服装平均每天可售出20件,每件盈利40元,为迎接“十、一”黄金周,商厦决定采取适当的降价措施增加盈利的同时尽可能减少库存,经市场调查发现:如果每件该品牌的童装每降价4元,那么平均每天就可多售出8件,要想平均每天在销售这种服装上盈利1200元,每件这种服装应降价多少元销售?
(1)利用表格分析数量关系:(若设应降价x元销售,请用代数式表示三处“?”)
(2)列方程求每件这种服装应降价多少元销售.
(1)利用表格分析数量关系:(若设应降价x元销售,请用代数式表示三处“?”)
| 有关数量 不同状态 | 日销售(件) | 单件利润(元) | 总利润(元) |
| ①原来的销售情况 |  |  | 20×40 |
| ②预期的销售情况 | 1200 |
 已知A、B两地相距80km,甲、乙两人沿同一条道路从A地到B地,l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.
已知A、B两地相距80km,甲、乙两人沿同一条道路从A地到B地,l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.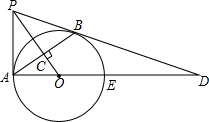 如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D.
如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA、AO,并延长AO交⊙O于点E,与PB的延长线交于点D. 一种长方形餐桌的四周可以坐6人用餐(带阴影的小长方形表示1个人的位置),现把n张这样的餐桌按如图方式拼接起来.
一种长方形餐桌的四周可以坐6人用餐(带阴影的小长方形表示1个人的位置),现把n张这样的餐桌按如图方式拼接起来.