题目内容
19.解方程组$\left\{\begin{array}{l}{5{x}^{2}-4{y}^{2}=20}\\{\sqrt{15}x-6y=2\sqrt{15}}\end{array}\right.$.
分析 由方程②变形得y=$\frac{\sqrt{15}}{6}$x-$\frac{\sqrt{15}}{3}$,代入①消去未知数y,解关于x的一元二次方程即可得.
解答 解:在方程组$\left\{\begin{array}{l}{5{x}^{2}-4{y}^{2}=20}&{①}\\{\sqrt{15}x-6y=2\sqrt{15}}&{②}\end{array}\right.$,
由②得:y=$\frac{\sqrt{15}}{6}$x-$\frac{\sqrt{15}}{3}$ ③,
把③代入①得:5x2-4($\frac{\sqrt{15}}{6}$x-$\frac{\sqrt{15}}{3}$)2=20,整理得:x2+2x-8=0,
解得:x1=2,x2=-4,
代入③得:y1=0,y2=-$\sqrt{15}$,
∴方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-4}\\{y=-\sqrt{15}}\end{array}\right.$.
点评 本题主要考查解高次方程组的能力,解方程组的消元思想是根本,灵活运用加减消元或代入消元方法是解题的关键.

练习册系列答案
相关题目
11.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 2,3,4 | C. | 6,7,8 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
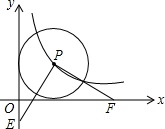 如图,点P为反比例函数y=$\frac{1}{x}$(x>0)图象上一点,以点P为圆心作圆,且该圆恰与两坐标轴都相切.在y轴任取一点E,连接PE并过点P作直线PE的垂线与x轴交于点F,则线段OE与线段OF的长度可能满足的数量关系式是OF-OE=2或OE-OF=2或OF+OE=2.
如图,点P为反比例函数y=$\frac{1}{x}$(x>0)图象上一点,以点P为圆心作圆,且该圆恰与两坐标轴都相切.在y轴任取一点E,连接PE并过点P作直线PE的垂线与x轴交于点F,则线段OE与线段OF的长度可能满足的数量关系式是OF-OE=2或OE-OF=2或OF+OE=2.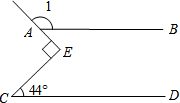 如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1=134°.
如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1=134°.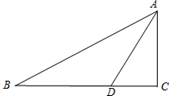 如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角分线.
如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角分线. 如图,四边形ABCD是矩形,将矩形折叠,使得点D落在BC边上.折痕经过点A,作出折叠后的图形(要求尺规作图,保留作图痕迹,不写作法)
如图,四边形ABCD是矩形,将矩形折叠,使得点D落在BC边上.折痕经过点A,作出折叠后的图形(要求尺规作图,保留作图痕迹,不写作法)