Question

1．已知正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A旋转．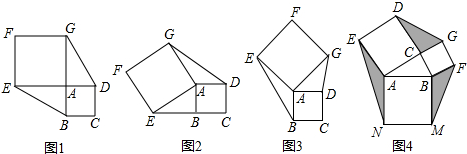

（1）发现与证明：当E点旋转到DA的延长线上时（如图1），△ABE与△ADG的面积关系是：相等
当E点旋转到CB的延长线上时（如图2），△ABE与△ADG的面积关系是：相等
（2）引申与运用：当正方形AEFG旋转任意一个角度时（如图3），△ABE与△ADG的面积关系是相等
并证明．
运用：已知△ABC，AB=5cm，BC=3cm，分别以AB、BC、CA为边向外作正方形（如图4），则图中阴影部分的面积和的最大值是18cm²．

Answer 1

分析 （1）①根据正方形的性质得到AE=AG，AB=AD，∠EAB=∠GAD，根据“SAS”可判断△ABE≌△ADG，则△ABE的面积=△ADG的面积；
②作GH⊥DA交DA的延长线于H，根据等角的余角相等得到∠GAH=∠EAB，根据“AAS”可判断△AHG≌△AEP，则GH=BP，然后根据三角形面积公式得到△ABE的面积=△ADG的面积；
（2）作GH⊥DA交DA的延长线于H，EP⊥BA交BA的延长线于P，根据等角的余角相等得到∠PAE=∠GAH，根据“AAS”可判断△AHG≌△AEP，所以GH=BP，然后根据三角形面积公式得到△ABP的面积=△ADG的面积；
运用：先根据勾股定理可计算出AC=4cm，则△ABC的面积=$\frac{1}{2}$×3×4=6（cm²）；然后根据（2）中的结结论计算阴影部分的面积和的最大值．

解答 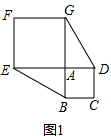解：（1）①∵正方形ABCD和正方形AEFG有公顶点A，将正方形AEFG绕点A旋转，E点旋转到DA的延长线上，
∴AE=AG，AB=AD，∠EAB=∠GAD，
∴△ABE≌△ADG（SAS），
∴△ABE的面积=△ADG的面积；
②作GH⊥DA交DA的延长线于H，如图2，
∴∠AHG=90°，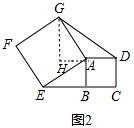
∵E点旋转到CB的延长线上，
∴∠ABE=90°，∠HAB=90°，
∴∠GAH=∠EAB，
在△AHG和△AEB中
$\left\{\begin{array}{l}{∠AHG=∠ABE}\\{∠GAH=∠EAB}\\{AG=AE}\end{array}\right.$，
∴△AHG≌△AEB，
∴GH=BE，
∵△ABE的面积=$\frac{1}{2}$EB•AB，△ADG的面积=$\frac{1}{2}$GH•AD，
∴△ABE的面积=△ADG的面积；

（2）结论仍然成立．理由如下：
作GH⊥DA交DA的延长线于H，EP⊥BA交BA的延长线于P，如图3，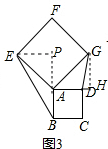
∵∠PAD=90°，∠EAG=90°，
∴∠PAE=∠GAH，
在△AHG和△AEP中
$\left\{\begin{array}{l}{∠GAH=∠EAP}\\{∠GHA=∠EPA}\\{AG=AE}\end{array}\right.$，
∴△AHG≌△AEP（AAS），
∴GH=BP，
∵△ABP的面积=$\frac{1}{2}$EP•AB，△ADG的面积=$\frac{1}{2}$GH•AD，
∴△ABP的面积=△ADG的面积；
运用：∵AB=5cm，BC=3cm，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4cm，
∴△ABC的面积=$\frac{1}{2}$×3×4=6（cm²）；
根据（2）中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=18cm²．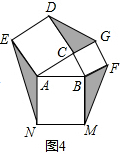
故答案为相等；相等；相等；18．

点评 本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；全等三角形的对应边相等．也考查了正方形的性质和三角形面积公式．