题目内容

11．下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（　　）
A．$\sqrt{3}$，$\sqrt{4}$，$\sqrt{5}$B．2，3，4C．6，7，8D．1，$\sqrt{2}$，$\sqrt{3}$

分析 欲判断是否是直角三角形，则需满足较小两边平方的和等于最大边的平方．

解答 解：A、（$\sqrt{3}$）2+（$\sqrt{4}$）2≠（$\sqrt{5}$）2，故不是直角三角形；
B、22+32≠42，故不是直角三角形；
C、62+72≠82，故不是直角三角形；
D、12+（$\sqrt{2}$）2=（$\sqrt{3}$）2，故是直角三角形；
故选：D．

点评 此题主要考查了勾股定理逆定理，关键是掌握如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．

练习册系列答案
相关题目
1．解方程：$\frac{2x-1}{3}$-$\frac{6x+1}{6}$=1．
2．定义：有一个内角为90°，且对角线相等的四边形称为准矩形．

（1）①如图1，准矩形ABCD中，∠ABC=90°，若AB=2，BC=3，则BD=$\sqrt{13}$；
②如图2，直角坐标系中，A（0，3），B（5，0），若整点P使得四边形AOBP是准矩形，则点P的坐标是（5，3），（3，5）；（整点指横坐标、纵坐标都为整数的点）
（2）如图3，正方形ABCD中，点E、F分别是边AD、AB上的点，且CF⊥BE，求证：四边形BCEF是准矩形；
（3）已知，准矩形ABCD中，∠ABC=90°，∠BAC=60°，AB=2，当△ADC为等腰三角形时，请直接写出这个准矩形的面积是$\sqrt{15}$+$\sqrt{3}$，$\sqrt{39}$+$\sqrt{3}$，2$\sqrt{15}$．
19．解方程组
$\left\{\begin{array}{l}{5{x}^{2}-4{y}^{2}=20}\\{\sqrt{15}x-6y=2\sqrt{15}}\end{array}\right.$．
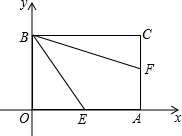6．如图，四边形的顶点O在平面直角坐标系的原点，顶点A、B分别在x轴、y轴上，OB∥AC，OB=AC．
（1）求证：四边形OACB是矩形；
（2）若点E是边OA的中点，且∠OBE=∠EBF，试探究线段AF、AC、BF之间的数量关系，并说明理由；
（3）在（2）条件下，若BE=8，BF=10，求点F的坐标．
16．在正方形ABCD中，连接BD．
（1）如图1，AE⊥BD于E．直接写出∠BAE的度数．
（2）如图1，在（1）的条件下，将△AEB以A旋转中心，沿逆时针方向旋转30°后得到△AB′E′，AB′与BD交于M，AE′的延长线与BD交于N．
①依题意补全图1；
②用等式表示线段BM、DN和MN之间的数量关系，并证明．
（3）如图2，E、F是边BC、CD上的点，△CEF周长是正方形ABCD周长的一半，AE、AF分别与BD交于M、N，写出判断线段BM、DN、MN之间数量关系的思路．（不必写出完整推理过程）
3．已知一个零刻度落在点A的量角器（半圆O）的直径为AB，等腰直角△BCD绕点B旋转．
（1）如图1，当等腰直角△BCD运动至斜边BD交量角器边缘于点G，直角边CD交量角器边缘于点E，F，第三边交量角器边缘于点H时，点G在量角器上的读数为20°，求此时点H在量角器上的读数．
（2）如图2，当点G，E在量角器上的读数α，β满足什么关系时，等腰直角△BCD的直角边CD会与半圆O相切于点E？请说明理由．
20．一次函数y=（m2-4）x+（m-1）和y=（m-1）x+m-5的图象与y轴分别交于点P和点Q，若点P与点Q关于x轴对称，则m=3．
13．与2$\sqrt{6}$-1最接近的整数是（　　）
A．3B．4C．5D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网