题目内容

14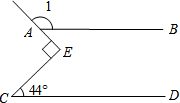．如图，直线AB∥CD，∠C=44°，∠E为直角，则∠1=134°．

分析 过E作EF∥AB，求出AB∥CD∥EF，根据平行线的性质得出∠C=∠FEC，∠BAE=∠FEA，求出∠BAE，即可求出答案．

解答 解：过E作EF∥AB，
∵AB∥CD，
∴AB∥CD∥EF，
∴∠C=∠FEC，∠BAE=∠FEA，
∵∠C=44°，∠AEC为直角，
∴∠FEC=44°，∠BAE=∠AEF=90°-44°=46°，
∴∠1=180°-∠BAE=180°-46°=134°，
故答案为：134°．

点评 本题考查了平行线的性质的应用，能正确作出辅助线是解此题的关键．

练习册系列答案
相关题目
4．用科学记数法表示0.000012=1.2×10-5．
5．下列真命题中，它的逆命题也是真命题的是（　　）
A．全等三角形的对应角相等
B．对顶角相等
C．等边三角形是锐角三角形
D．直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半
2．定义：有一个内角为90°，且对角线相等的四边形称为准矩形．

（1）①如图1，准矩形ABCD中，∠ABC=90°，若AB=2，BC=3，则BD=$\sqrt{13}$；
②如图2，直角坐标系中，A（0，3），B（5，0），若整点P使得四边形AOBP是准矩形，则点P的坐标是（5，3），（3，5）；（整点指横坐标、纵坐标都为整数的点）
（2）如图3，正方形ABCD中，点E、F分别是边AD、AB上的点，且CF⊥BE，求证：四边形BCEF是准矩形；
（3）已知，准矩形ABCD中，∠ABC=90°，∠BAC=60°，AB=2，当△ADC为等腰三角形时，请直接写出这个准矩形的面积是$\sqrt{15}$+$\sqrt{3}$，$\sqrt{39}$+$\sqrt{3}$，2$\sqrt{15}$．
9．已知关于x的方程ax+b=0，有以下四种说法：
①若x=1是该方程的解，则a+b=0；②若a=-1，则x=b是该方程的解；
③若a≠0，则该方程的解是x=-$\frac{b}{a}$；④若a=0，b≠0，则该方程无解．
其中所有正确说法的序号是①②③④．
19．解方程组
$\left\{\begin{array}{l}{5{x}^{2}-4{y}^{2}=20}\\{\sqrt{15}x-6y=2\sqrt{15}}\end{array}\right.$．
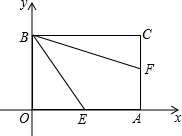6．如图，四边形的顶点O在平面直角坐标系的原点，顶点A、B分别在x轴、y轴上，OB∥AC，OB=AC．
（1）求证：四边形OACB是矩形；
（2）若点E是边OA的中点，且∠OBE=∠EBF，试探究线段AF、AC、BF之间的数量关系，并说明理由；
（3）在（2）条件下，若BE=8，BF=10，求点F的坐标．
3．已知一个零刻度落在点A的量角器（半圆O）的直径为AB，等腰直角△BCD绕点B旋转．
（1）如图1，当等腰直角△BCD运动至斜边BD交量角器边缘于点G，直角边CD交量角器边缘于点E，F，第三边交量角器边缘于点H时，点G在量角器上的读数为20°，求此时点H在量角器上的读数．
（2）如图2，当点G，E在量角器上的读数α，β满足什么关系时，等腰直角△BCD的直角边CD会与半圆O相切于点E？请说明理由．
16．已知点A（0，4），B在x轴上，且AB=5，则点B的坐标是（3，0）或（-3，0）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网