题目内容
15．不等式组$\left\{\begin{array}{l}{2x≥x-3}\\{\frac{x+2}{3}＞x}\end{array}\right.$的解集为（ ）| A． | x≥-3 | B． | x＜1 | C． | -3≤x＜1 | D． | x＞1 |
分析 分别求出不等式组中两不等式的解集，找出两解集的公共部分即可．
解答 解：$\left\{\begin{array}{l}{2x≥x-3①}\\{\frac{x+2}{3}＞x②}\end{array}\right.$，
由①得：x≥-3，
由②得：x＜1，
则不等式组的解集为-3≤x＜1，
故选C
点评 此题考查了解一元一次不等式组，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
说理过程填空：
3．已知点P（x，|x|），则点P一定（ ）
| A． | 在第一象限 | B． | 不在y轴上 | C． | 在x轴上方 | D． | 不在x轴下方 |
10．
如图，直线m∥n，Rt△ABC的顶点A在直线n上，∠C=90°，若∠1=25°，∠2=70°，则∠B=（ ）
如图，直线m∥n，Rt△ABC的顶点A在直线n上，∠C=90°，若∠1=25°，∠2=70°，则∠B=（ ）| A． | 65° | B． | 55° | C． | 45° | D． | 35° |
20．下列各式是最简二次根式的是（ ）
| A． | $\sqrt{{m}^{2}+1}$ | B． | $\sqrt{a{b}^{5}}$ | C． | $\sqrt{12}$ | D． | $\sqrt{\frac{1}{3}}$ |
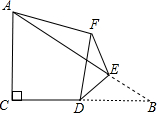如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=6，点D是边BC的中点，点E是边AB上的任意一点（点E不与点B重合），沿DE翻折△DBE使点B落在点F处，连接AF，则线段AF的长取最小值时，BF的长为$\frac{12\sqrt{5}}{5}$．