题目内容
12.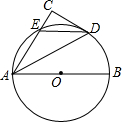 如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE
如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE(1)求证:AD平分∠CAB
(2)若CE=2,sin∠EAD=$\frac{\sqrt{5}}{5}$,求⊙O的半径OA的长.
分析 (1)连接OD,如图,利用切线的性质得OD⊥CD,则可判断OD∥AC,所以∠CAD=∠ODA,加上∠OAD=∠ODA,于是得到∠OAD=∠CAD;
(2)连接BD,如图,利用圆周角定理得到∠ADB=90°,∠CED=∠B,则∠BAD=∠CDE,所以sin∠BAD=sin∠CDE=sin∠EAD=$\frac{\sqrt{5}}{5}$,在Rt△CDE中,利用正弦可计算出sDE=2$\sqrt{5}$,再证明DE=BD=2$\sqrt{5}$,然后在Rt△ABD中利用正弦的定义可求出AB,从而得到OA的长.
解答 (1)证明:连接OD,如图,
∵CD与⊙O相切与点D,
∴OD⊥CD,
∵AC⊥CD,
∴OD∥AC,
∴∠CAD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠OAD=∠CAD,
即AD平分∠CAB;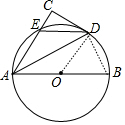
(2)解:连接BD,如图,
∵AB为直径,
∴∠ADB=90°,
∵∠CED=∠B,
∴∠BAD=∠CDE,
而∠BAD=∠CAD,
∴sin∠BAD=sin∠CDE=sin∠EAD=$\frac{\sqrt{5}}{5}$,
在Rt△CDE中,sin∠CDE=$\frac{CE}{DE}$=$\frac{\sqrt{5}}{5}$,
∴DE=$\frac{2×5}{\sqrt{5}}$=2$\sqrt{5}$,
∴$\widehat{DE}$=$\widehat{BD}$,
∴DE=BD=2$\sqrt{5}$,
在Rt△ABD中,sin∠BAD=$\frac{BD}{AB}$=$\frac{\sqrt{5}}{5}$,
∴AB=$\frac{2\sqrt{5}×5}{\sqrt{5}}$=10,
∴OA=$\frac{1}{2}$AB=5.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了解直径三角形.

 阅读快车系列答案
阅读快车系列答案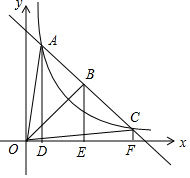 如图,直线l与函数y=$\frac{k}{x}$的图象相交,A、B、C是直线l的三点,过点A、B、C分别作x轴的垂线,垂足分别为D、E、F,连接OA、OB、OC,设△OAD的面积是S1,△OBE的面积是S2,△OCF的面积是S3,则( )
如图,直线l与函数y=$\frac{k}{x}$的图象相交,A、B、C是直线l的三点,过点A、B、C分别作x轴的垂线,垂足分别为D、E、F,连接OA、OB、OC,设△OAD的面积是S1,△OBE的面积是S2,△OCF的面积是S3,则( )| A. | S1<S2<S3 | B. | S1=S2=S3 | C. | S2>S1>S3 | D. | S3=S1<S2 |
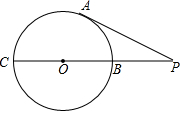 如图,PA切⊙O于点A,PC过点O且交⊙O于点B、C,若PA=3,PB=2,则⊙O 的半径为$\frac{5}{4}$.
如图,PA切⊙O于点A,PC过点O且交⊙O于点B、C,若PA=3,PB=2,则⊙O 的半径为$\frac{5}{4}$.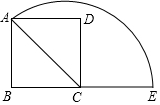 如图,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC长为半径画弧,与BC的延长线交于点E,则图中$\widehat{AE}$的长为$\frac{3\sqrt{2}}{2}$π.
如图,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC长为半径画弧,与BC的延长线交于点E,则图中$\widehat{AE}$的长为$\frac{3\sqrt{2}}{2}$π.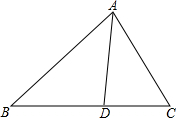 (1)求证:角平分线上的点到这个角的两边的距离相等.
(1)求证:角平分线上的点到这个角的两边的距离相等. 如图,在平面直角坐标系中,圆M经过原点O,直线y=-$\frac{3}{4}$x-6与x轴、y轴分别相交于A,B两点.
如图,在平面直角坐标系中,圆M经过原点O,直线y=-$\frac{3}{4}$x-6与x轴、y轴分别相交于A,B两点.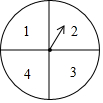 由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.
由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.