题目内容
2.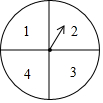 由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.
由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.如果小王和小张按上述规则各转动转盘一次,则
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
分析 (1)根据概率公式直接计算即可;
(2)列表得出所有等可能的情况数,找出两指针所指数字都是偶数或都是奇数的概率即可得知该游戏是否公平.
解答 解:
(1)∵转盘的4个等分区域内只有1,3两个奇数,
∴小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率=$\frac{2}{4}$=$\frac{1}{2}$;
(2)列表如下:
| 1 | 2 | 3 | 4 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) |
∴P(小王胜)=$\frac{4}{16}$=$\frac{1}{4}$,P(小张胜)=$\frac{4}{16}$=$\frac{1}{4}$,
∴游戏公平.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
17.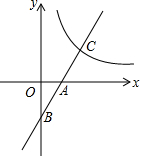 如图,已知一次函数y=kx-3(k≠0)的图象与x轴,y轴分别交于A,B两点,与反比例函数y=$\frac{12}{x}$(x>0)交于C点,且AB=AC,则k的值为$\frac{3}{2}$.
如图,已知一次函数y=kx-3(k≠0)的图象与x轴,y轴分别交于A,B两点,与反比例函数y=$\frac{12}{x}$(x>0)交于C点,且AB=AC,则k的值为$\frac{3}{2}$.
 如图,已知一次函数y=kx-3(k≠0)的图象与x轴,y轴分别交于A,B两点,与反比例函数y=$\frac{12}{x}$(x>0)交于C点,且AB=AC,则k的值为$\frac{3}{2}$.
如图,已知一次函数y=kx-3(k≠0)的图象与x轴,y轴分别交于A,B两点,与反比例函数y=$\frac{12}{x}$(x>0)交于C点,且AB=AC,则k的值为$\frac{3}{2}$.
14.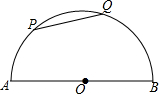 如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,则$\widehat{AP}$与$\widehat{QB}$的长度之和为( )
如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,则$\widehat{AP}$与$\widehat{QB}$的长度之和为( )
 如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,则$\widehat{AP}$与$\widehat{QB}$的长度之和为( )
如图,半圆O的直径AB=4,P,Q是半圆O上的点,弦PQ的长为2,则$\widehat{AP}$与$\widehat{QB}$的长度之和为( )| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | π |
11.在我市开展的“好书伴我成长”读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如表所示:
(1)求这次调查的50名学生读书的册数的平均数和众数.
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 3 | 13 | 16 | 17 | 1 |
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.
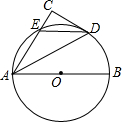 如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE
如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE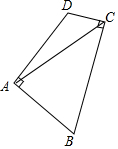 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为18.
如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=6,则四边形ABCD的面积为18. 已知:△ABC.
已知:△ABC.