题目内容
7. 如图,在平面直角坐标系中,圆M经过原点O,直线y=-$\frac{3}{4}$x-6与x轴、y轴分别相交于A,B两点.
如图,在平面直角坐标系中,圆M经过原点O,直线y=-$\frac{3}{4}$x-6与x轴、y轴分别相交于A,B两点.(1)求出A,B两点的坐标;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交x轴于D、E两点,在抛物线上是否存在点P,使得
S△PDE=$\frac{1}{10}$S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
分析 (1)根据一次函数与坐标轴交点坐标求法得出答案即可;
(2)利用顶点式由B点坐标求出二次函数解析式即可;
(3)首先求出△ABC的面积,进而求出D,E坐标,设P(t,-$\frac{1}{2}$x2-4x-6),根据S△PDE=$\frac{1}{10}$S△ABC,得到|-$\frac{1}{2}$t2-4t-6|=1,分两种情况讨论即可求出P点坐标.
解答 解:(1)对于直线y=-$\frac{3}{4}$x-6,
当x=0,y=-6;
当y=0,得0=-$\frac{3}{4}$x-6,解得x=-8.
故A(-8,0),B(0,-6);
(2)在Rt△AOB中,AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵∠AOB=90°,
∴AB为⊙M的直径,
∴点M为AB的中点,M(-4,-3),
∵MC∥y轴,MC=5,
∴C(-4,2),
设抛物线的解析式为y=a(x+4)2+2,
把B(0,-6)代入得16a+2=-6,解得a=-$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$(x+4)2+2,即y=-$\frac{1}{2}$x2-4x-6,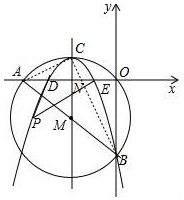 (3)存在.
(3)存在.
如图,当y=0时,-$\frac{1}{2}$(x+4)2+2=0,解得x1=-2,x2=-6,
∴D(-6,0),E(-2,0),
S△ABC=S△ACM+S△BCM=$\frac{1}{2}$×CM×8=20,
设P(t,-$\frac{1}{2}$x2-4x-6),
∵S△PDE=$\frac{1}{10}$S△ABC,
∴$\frac{1}{2}$(-2+6)|-$\frac{1}{2}$t2-4t-6|=$\frac{1}{10}$×20,
即|-$\frac{1}{2}$t2-4t-6|=1,
当-$\frac{1}{2}$t2-4t-6=-1,解得t1=-4+$\sqrt{6}$,t2=-4-$\sqrt{6}$,此时P点坐标为(-4+$\sqrt{6}$,-1)或(-4-$\sqrt{6}$,-1);
当-$\frac{1}{2}$t2-4t-6=1,解得t1=-4+$\sqrt{2}$,t2=-4-$\sqrt{2}$,此时P点坐标为(-4+$\sqrt{2}$,1)或(-4-$\sqrt{2}$,1).
综上所述,P点坐标为(-4+$\sqrt{6}$,-1)或(-4-$\sqrt{6}$,-1)或(-4+$\sqrt{2}$,1)或(-4-$\sqrt{2}$,1)时,使得S△PDE=$\frac{1}{10}$S△ABC.
点评 此题主要考查了二次函数的综合应用以及顶点式求二次函数解析式和一元二次方程的解法,此题综合性较强,用到分类讨论思想,注意不要漏解.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案| A. |  | B. |  | C. |  | D. |  |
我们借助学习“图形的判定”获得的经验与方法对“平行四边形的判定”进一步探究.
【初步思考】
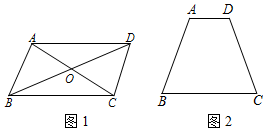
在一个四边形中,我们把“一组对边平行、一组对边相等、一组对角相等或一条对角线被另一条对角线平分”称为一个条件.如图1,四边形ABCD中,我们用符号语言表示出所有的8个条件:
| ①AB=CD; | ②AD=BC; | ③AB∥CD; | ④AD∥BC; |
| ⑤∠BAD=∠BCD; | ⑥∠ABC=∠ADC; | ⑦OA=OC; | ⑧OB=OD. |
【深入探究】
小莉所在学习小组进行了研究,她们认为2个条件可分为以下六种类型:
Ⅰ关于对边的2个条件;Ⅱ关于对角的2个条件;
Ⅲ关于对角线的2个条件;Ⅳ关于边的条件与角的条件各1个;
Ⅴ关于边的条件与对角线的条件各1个;Ⅵ关于角的条件与对角线的条件各1个.
(1)小明认为“Ⅰ关于对边的2个条件”可分为“①②,③④,①③,①④”共4种不同种类的情形.请你仿照小明的叙述对其它五种类型进一步分类.
(2)小红认为有4种情形是平行四边形的判定依据.请你写出其它的三个判定定理.
定义:两组对边分别平行的四边形是平行四边形;
定理1:两组对边分别相等的四边形是平行四边形;
定理2:一组对边平行且相等的四边形是平行四边形;
定理3:对角线互相平分的四边形是平行四边形.
(3)小刚认为除了4个判定依据外,还存在一些真命题,他写出了其中的1个,请证明这个真命题,并仿照他的格式写出其它真命题(无需证明):
真命题1:四边形ABCD中,若∠BAD=∠BCD,∠ABC=∠ADC,则四边形ABCD是平行四边形.
(4)小亮认为,还存在一些假命题,他写出了其中的1个,并举反例进行了说明,请你仿照小亮的格式写出其它假命题并举反例进行说明.
假命题1:四边形ABCD中,若AB=CD,AD∥BC,则四边形ABCD不一定是平行四边形.
反例说明:如图2,四边形ABCD中,AB=CD,AD∥BC,显然四边形ABCD不是平行四边形.
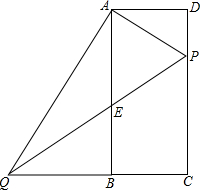 已知矩形ABCD中,AD=6,AB=12,P为边CD上的动点,过A点作AQ⊥AP,交CB的延长线于点Q,交AB于点E,若DP=x,CQ=y,
已知矩形ABCD中,AD=6,AB=12,P为边CD上的动点,过A点作AQ⊥AP,交CB的延长线于点Q,交AB于点E,若DP=x,CQ=y,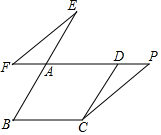 如图,在平行四边形ABCD中,延长BA至点E,使AE=AB,点F、P在边AD所在的直线上,EF∥CP.
如图,在平行四边形ABCD中,延长BA至点E,使AE=AB,点F、P在边AD所在的直线上,EF∥CP.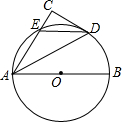 如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE
如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE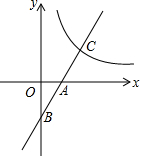 如图,已知一次函数y=kx-3(k≠0)的图象与x轴,y轴分别交于A,B两点,与反比例函数y=$\frac{12}{x}$(x>0)交于C点,且AB=AC,则k的值为$\frac{3}{2}$.
如图,已知一次函数y=kx-3(k≠0)的图象与x轴,y轴分别交于A,B两点,与反比例函数y=$\frac{12}{x}$(x>0)交于C点,且AB=AC,则k的值为$\frac{3}{2}$.