题目内容
3.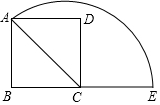 如图,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC长为半径画弧,与BC的延长线交于点E,则图中$\widehat{AE}$的长为$\frac{3\sqrt{2}}{2}$π.
如图,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC长为半径画弧,与BC的延长线交于点E,则图中$\widehat{AE}$的长为$\frac{3\sqrt{2}}{2}$π.
分析 先利用正方形的性质得到CA=$\sqrt{2}$AB=2$\sqrt{2}$,∠ACB=45°,则利用互补得到∠ACE=135°,然后根据弧长公式计算$\widehat{AE}$的长度.
解答 解:∵四边形ABCD为正方形,
∴CA=$\sqrt{2}$AB=2$\sqrt{2}$,∠ACB=45°,
∴∠ACE=135°,
∴$\widehat{AE}$的长度=$\frac{135•π•2\sqrt{2}}{180}$=$\frac{3\sqrt{2}}{2}$π.
故答案为$\frac{{3\sqrt{2}}}{2}π$.
点评 本题考查了弧长公式:l=$\frac{n•π•R}{180}$(弧长为l,圆心角度数为n,圆的半径为R).

练习册系列答案
相关题目
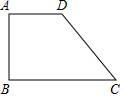 如图,梯形ABCD中,∠ABC=∠BAD=90°,AD=AB=1,∠BCD=45°.将梯形ABCD折叠,使得点C与点A重合,折痕交CD于E,交BC于F,画出图形.求出折叠后重叠部分的面积.
如图,梯形ABCD中,∠ABC=∠BAD=90°,AD=AB=1,∠BCD=45°.将梯形ABCD折叠,使得点C与点A重合,折痕交CD于E,交BC于F,画出图形.求出折叠后重叠部分的面积.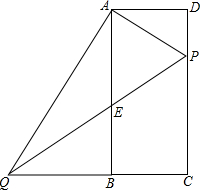 已知矩形ABCD中,AD=6,AB=12,P为边CD上的动点,过A点作AQ⊥AP,交CB的延长线于点Q,交AB于点E,若DP=x,CQ=y,
已知矩形ABCD中,AD=6,AB=12,P为边CD上的动点,过A点作AQ⊥AP,交CB的延长线于点Q,交AB于点E,若DP=x,CQ=y, 已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB、AC的中点,求证:BE=CD.
已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB、AC的中点,求证:BE=CD.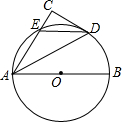 如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE
如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE