题目内容
1.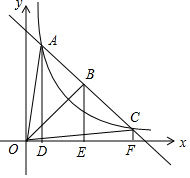 如图,直线l与函数y=$\frac{k}{x}$的图象相交,A、B、C是直线l的三点,过点A、B、C分别作x轴的垂线,垂足分别为D、E、F,连接OA、OB、OC,设△OAD的面积是S1,△OBE的面积是S2,△OCF的面积是S3,则( )
如图,直线l与函数y=$\frac{k}{x}$的图象相交,A、B、C是直线l的三点,过点A、B、C分别作x轴的垂线,垂足分别为D、E、F,连接OA、OB、OC,设△OAD的面积是S1,△OBE的面积是S2,△OCF的面积是S3,则( )| A. | S1<S2<S3 | B. | S1=S2=S3 | C. | S2>S1>S3 | D. | S3=S1<S2 |
分析 根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=$\frac{1}{2}$|k|.
解答 解:结合题意可得:A、C都在双曲线y=$\frac{k}{x}$上,
则有S1=S3;
而AC之间,直线在双曲线上方;
故S1=S3<S2.
故选:D.
点评 本题主要考查了反比例函数y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
相关题目
11.在我市开展的“好书伴我成长”读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如表所示:
(1)求这次调查的50名学生读书的册数的平均数和众数.
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 3 | 13 | 16 | 17 | 1 |
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.
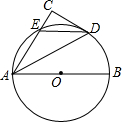 如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE
如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE