题目内容
20. (1)求证:角平分线上的点到这个角的两边的距离相等.
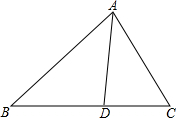
(1)求证:角平分线上的点到这个角的两边的距离相等.(2)如图,AD是△ABC的角平分线,求证:$\frac{AB}{AC}$=$\frac{BD}{CD}$.
分析 (1)先写出已知、求证,根据角平分线的定义得到∠POE=∠POF,由垂直的定义得∠PEO=∠PFO=90°,易证得△PEO≌△PFO,根据三角形全等的性质即可得到PE=PF;
(2)先过点B作BE∥AC交AD延长线于点E,由于BE∥AC,利用平行线分线段成比例定理的推论、平行线的性质,可得△BDE∽△CDA,∠E=∠DAC,再利用相似三角形的性质可有$\frac{BD}{CD}=\frac{BE}{AC}$,而利用AD时角平分线又知∠E=∠DAC=∠BAD,于是BE=AB,等量代换即可证.
解答  解:已知:OC平分∠AOB,点P为OC上任一点,PE⊥OA于E,PF⊥OB于F.
解:已知:OC平分∠AOB,点P为OC上任一点,PE⊥OA于E,PF⊥OB于F.
求证:PE=PF已知:OC平分∠AOB,点P为OC上任一点,PE⊥OA于E,PF⊥OB于F.
求证:PE=PF
证明:∵OC平分∠AOB,
∴∠POE=∠POF,
∵PE⊥OA于E,PF⊥OB于F,
∴∠PEO=∠PFO=90°,
在△PEO和△PFO中$\left\{\begin{array}{l}{∠PEO=∠PFO}\\{∠POE=∠POF}\\{OP=OP}\end{array}\right.$,
∴△PEO≌△PFO(AAS),
∴PE=PF,
∴角平分线上的点到这个角的两边的距离相等;
(2)如图
过点B作BE∥AC交AD延长线于点E,
∵BE∥AC,
∴∠DBE=∠C,∠E=∠CAD,
∴△BDE∽△CDA,
∴$\frac{BD}{CD}=\frac{BE}{AC}$,
又∵AD是角平分线,
∴∠E=∠DAC=∠BAD,
∴BE=AB,
∴$\frac{AB}{AC}$=$\frac{BD}{CD}$.
点评 本题考查了角平分线的性质:角平分线上的点到角的两边的距离相等.也考查了三角形全等的判定与性质.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
16.几个相同的小正方体所搭成的几何体的俯视图如图所示,小正方形中的数字表示在该位置小正方体的个数最多是( )
俯视图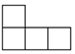 左视图
左视图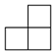
俯视图
 左视图
左视图
| A. | 5个 | B. | 7个 | C. | 8个 | D. | 9个 |
 已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB、AC的中点,求证:BE=CD.
已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB、AC的中点,求证:BE=CD. 在2017年的理化生实验考试中某校6名学生的实验成绩统计如图,这组数据的众数是26分.
在2017年的理化生实验考试中某校6名学生的实验成绩统计如图,这组数据的众数是26分.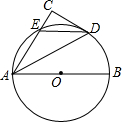 如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE
如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE