题目内容
2.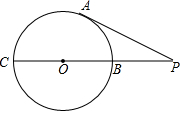 如图,PA切⊙O于点A,PC过点O且交⊙O于点B、C,若PA=3,PB=2,则⊙O 的半径为$\frac{5}{4}$.
如图,PA切⊙O于点A,PC过点O且交⊙O于点B、C,若PA=3,PB=2,则⊙O 的半径为$\frac{5}{4}$.
分析 连接半径,⊙O的半径为r,根据勾股定理列方程可解决问题.
解答  解:连接OA,
解:连接OA,
∵PA切⊙O于点A,
∴OA⊥PA,
∴∠OAP=90°,
设⊙O的半径为r,则OA=OB=r,OP=r+2,
由勾股定理得:r2+32=(r+2)2,
r=$\frac{5}{4}$,
则⊙O 的半径为$\frac{5}{4}$;
故答案为:$\frac{5}{4}$.
点评 本题考查了切线的性质、勾股定理,熟练掌握圆的切线垂直于经过切点的半径.并与方程相结合,这是数学中求线段长常运用的方法.

练习册系列答案
相关题目
16.几个相同的小正方体所搭成的几何体的俯视图如图所示,小正方形中的数字表示在该位置小正方体的个数最多是( )
俯视图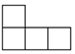 左视图
左视图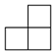
俯视图
 左视图
左视图
| A. | 5个 | B. | 7个 | C. | 8个 | D. | 9个 |
3.下列图形中,是轴对称图形,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
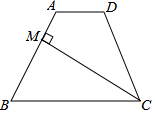 如图,四边形ABCD中,AD∥BC,CM是∠BCD的平分线,且CM⊥AB,M为垂足,AM=$\frac{1}{3}$AB.若四边形ABCD的面积为$\frac{15}{7}$,则四边形AMCD的面积是1.
如图,四边形ABCD中,AD∥BC,CM是∠BCD的平分线,且CM⊥AB,M为垂足,AM=$\frac{1}{3}$AB.若四边形ABCD的面积为$\frac{15}{7}$,则四边形AMCD的面积是1.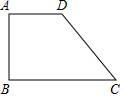 如图,梯形ABCD中,∠ABC=∠BAD=90°,AD=AB=1,∠BCD=45°.将梯形ABCD折叠,使得点C与点A重合,折痕交CD于E,交BC于F,画出图形.求出折叠后重叠部分的面积.
如图,梯形ABCD中,∠ABC=∠BAD=90°,AD=AB=1,∠BCD=45°.将梯形ABCD折叠,使得点C与点A重合,折痕交CD于E,交BC于F,画出图形.求出折叠后重叠部分的面积.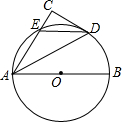 如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE
如图,AB为⊙O的直径,CD与⊙O相切与点D,AC⊥CD于C,并交⊙O于E,连接DE