题目内容
5.已知平行四边形ABCD的两邻边AB、AD的长是关于x的一元二次方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根.(1)当m为何值时,四边形ABCD是菱形?
(2)若AB的长为2,那么平行四边形ABCD的周长是多少?
分析 (1)根据菱形的性质可得出AB=AD,由根的判别式即可得出关于m的一元二次方程,解之即可得出m的值;
(2)将x=2代入一元二次方程可求出m的值,再根据根与系数的关系即可得出AB+AD的值,利用平行四边形的性质即可求出平行四边形ABCD的周长.
解答 解:(1)∵四边形ABCD是菱形,
∴AB=AD,
∵AB、AD的长是关于x的一元二次方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根,
∴△=(-m)2-4($\frac{m}{2}$-$\frac{1}{4}$)=m2-2m+1=0,
解得:m=1.
∴当m为1时,四边形ABCD是菱形.
(2)将x=2代入x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0中,得:4-2m+$\frac{m}{2}$-$\frac{1}{4}$=0,
解得:m=$\frac{5}{2}$,
∵AB、AD的长是关于x的一元二次方程x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0的两个实数根,
∴AB+AD=m=$\frac{5}{2}$,
∴平行四边形ABCD的周长=2(AB+AD)=2×$\frac{5}{2}$=5.
点评 本题考查了根的判别式、菱形的性质、平行四边形的性质以及根与系数的关系,解题的关键是:(1)根据根的判别式找出关于m的一元二次方程;(2)将x=2代入原方程求出m值.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
16.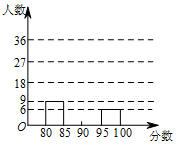 为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:
为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:
(1)请在图中补全频数分布直方图;
(2)抽取的这部分参赛同学成绩的中位数落在哪个分数段?
(3)如果该校参加人数1000人,请估计分数在95≤x<100段的人数约为多少?
 为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:
为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:| 分数段 | 频数 | 频率 |
| 80≤x<85 | 9 | 0.15 |
| 85≤x<90 | m | 0.45 |
| 90≤x<95 | ■ | ■ |
| 95≤x<100 | 6 | n |
(2)抽取的这部分参赛同学成绩的中位数落在哪个分数段?
(3)如果该校参加人数1000人,请估计分数在95≤x<100段的人数约为多少?
 在平面直角坐标系上画出y=2x-2的图象
在平面直角坐标系上画出y=2x-2的图象 已知A、B两地相距80km,甲、乙两人沿同一条道路从A地到B地,l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.
已知A、B两地相距80km,甲、乙两人沿同一条道路从A地到B地,l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.