题目内容
13.解方程:x2-4x-4=0.(用配方法解答)分析 移项后两边配上一次项系数一半的平方后求解可得.
解答 解:∵x2-4x=4,
∴x2-4x+4=4+4,即(x-2)2=8,
∴x-2=±2$\sqrt{2}$,
则x=2±2$\sqrt{2}$.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
8.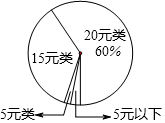 某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.
某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.
(1)求表中字母m的值及扇形统计图中“15元类”所对应的圆心角的度数.
(2)该校九年级共1200人,请估计捐款金额不低于15元的学生人数.
(3)据了解,样本中捐款金额为5元以下的同学的捐款金额为2元或1元,若从样本中捐款金额为5元以下的同学中随机抽取1位同学,求所抽同学的捐款金额为2元的概率.
 某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.
某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.| 类别 | 20元类 | 15元类 | 5元类 | 5元以下 |
| 各类合计捐款数 | 360 | m | 5 | 10 |
(2)该校九年级共1200人,请估计捐款金额不低于15元的学生人数.
(3)据了解,样本中捐款金额为5元以下的同学的捐款金额为2元或1元,若从样本中捐款金额为5元以下的同学中随机抽取1位同学,求所抽同学的捐款金额为2元的概率.
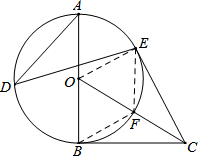 如图,以Rt△OBC的直角边OB为半径作⊙O,点D、E都在⊙O上,且∠ADE=∠OCB,连接CE.
如图,以Rt△OBC的直角边OB为半径作⊙O,点D、E都在⊙O上,且∠ADE=∠OCB,连接CE. 如图,AD∥BE∥CF,AB=6,BC=3,DF=8,求EF的长.
如图,AD∥BE∥CF,AB=6,BC=3,DF=8,求EF的长.