题目内容
15. 在平面直角坐标系上画出y=2x-2的图象
在平面直角坐标系上画出y=2x-2的图象(1)判断A(5,7),B($\frac{1}{8},-\frac{7}{4}$)是否在这一条直线上.
(2)若M(-5,m),N(n,2)在y=2x-2上,求$\sqrt{n-m}$的值.
分析 将x=0、y=0分别带人y=2x-2中求出与之对应的y、x值,描点、连线即可画出一次函数图象.
(1)将点A、B的x值代入一次函数解析式中求出与之对应的y值,比照后即可得知点A、B是否在该直线上;
(2)由点M、N在直线上,利用一次函数图象上点的坐标特征求出m、n的值,将其代入$\sqrt{n-m}$中即可得出结论.
解答 解:当x=0时,y=2x-2=-2,
∴y=2x-2的图象与y轴交于点(0,-2);
当y=2x-2=0时,x=1,
∴y=2x-2的图象与x轴交于点(1,0).
画出函数图象,如图所示.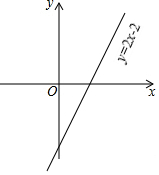
(1)当x=5时,y=2×5-2=8,
∴点A(5,7)不在该直线上;
当x=$\frac{1}{8}$时,y=2×$\frac{1}{8}$-2=-$\frac{7}{4}$,
∴点B($\frac{1}{8}$,-$\frac{7}{4}$)在该直线上.
(2)∵M(-5,m)、N(n,2)在直线y=2x-2上,
∴m=2×(-5)-2,2=2n-2,
∴m=-12,n=2.
∴$\sqrt{n-m}$=$\sqrt{2-(-12)}$=$\sqrt{14}$.
点评 本题考查了一次函数图象上点的坐标特征以及一次函数的图象,解题的关键是:(1)分别代入点A、B的横坐标求出y值;(2)根据一次函数图象上点的坐标特征求出m、n的值.

练习册系列答案
相关题目
5.下列命题的逆命题不正确的是( )
| A. | 同角的余角相等 | |
| B. | 等腰三角形的两个底角相等 | |
| C. | 两直线平行,内错角相等 | |
| D. | 线段中垂线上的点到线段两端的距离相等 |
10.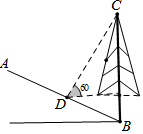 如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).
如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).
 如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).
如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).
20.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a3÷a=a3 | C. | (a2)3=a6 | D. | (3a3)3=9a9 |
7.二次函数y=x2+2x+4的最小值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 如图,为修通铁路凿通隧道AC,量出∠C=90°,AB=5公里,BC=4公里,若每天凿隧道0.3公里,问几天才能把隧道AC凿通?
如图,为修通铁路凿通隧道AC,量出∠C=90°,AB=5公里,BC=4公里,若每天凿隧道0.3公里,问几天才能把隧道AC凿通?