题目内容
16.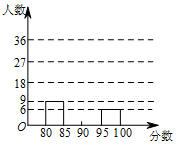 为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:
为活跃校园生活,某校开展了“我歌唱我快乐”海选比赛活动,抽取海选中部分参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如下:| 分数段 | 频数 | 频率 |
| 80≤x<85 | 9 | 0.15 |
| 85≤x<90 | m | 0.45 |
| 90≤x<95 | ■ | ■ |
| 95≤x<100 | 6 | n |
(2)抽取的这部分参赛同学成绩的中位数落在哪个分数段?
(3)如果该校参加人数1000人,请估计分数在95≤x<100段的人数约为多少?
分析 (1)根据统计表中,频数与频率的比值相等,可得关于m、n的关系式;进而计算可得m、n的值;进一步补全直方图;
(2)根据中位数的定义判断;
(3)根据频数=数据总和×频率,列式计算即可求解.
解答 解:(1)根据统计表中,频数与频率的比值相等,
即有$\frac{m}{0.45}$=$\frac{9}{0.15}$=$\frac{6}{n}$,
解得:m=27,n=0.1;
如图所示:
(2)根据中位数的求法,先将数据按从小到大的顺序排列,
读图可得:共60人,第30、31名都在85分~90分,
故抽取的这部分参赛同学成绩的中位数落在85分~90分的分数段.
(3)1000×0.1=100(人).
答:分数在95≤x<100段的人数约为100人.
点评 本题考查条形统计图、图表等知识.结合生活实际,绘制条形统计图或从统计图中获取有用的信息,是近年中考的热点.只要能认真准确读图,并作简单的计算,一般难度不大.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
7.二次函数y=x2+2x+4的最小值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
8.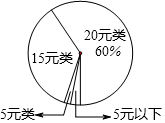 某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.
某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.
(1)求表中字母m的值及扇形统计图中“15元类”所对应的圆心角的度数.
(2)该校九年级共1200人,请估计捐款金额不低于15元的学生人数.
(3)据了解,样本中捐款金额为5元以下的同学的捐款金额为2元或1元,若从样本中捐款金额为5元以下的同学中随机抽取1位同学,求所抽同学的捐款金额为2元的概率.
 某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.
某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.| 类别 | 20元类 | 15元类 | 5元类 | 5元以下 |
| 各类合计捐款数 | 360 | m | 5 | 10 |
(2)该校九年级共1200人,请估计捐款金额不低于15元的学生人数.
(3)据了解,样本中捐款金额为5元以下的同学的捐款金额为2元或1元,若从样本中捐款金额为5元以下的同学中随机抽取1位同学,求所抽同学的捐款金额为2元的概率.
 如图,为修通铁路凿通隧道AC,量出∠C=90°,AB=5公里,BC=4公里,若每天凿隧道0.3公里,问几天才能把隧道AC凿通?
如图,为修通铁路凿通隧道AC,量出∠C=90°,AB=5公里,BC=4公里,若每天凿隧道0.3公里,问几天才能把隧道AC凿通?
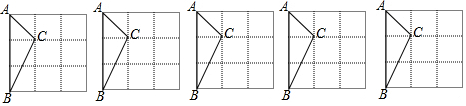
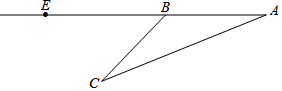 日前一渔船在南海打渔时遇险,并立即拨打了求救电话,警方接到电话立即派出直升机前去营救.飞机在空中A点看到渔船C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见渔船C的俯角为45°,已知飞机的飞行速度为3150米/分.(参考数据:tan20°≈0.3,cos20°≈0.9,sin20°≈0.2)
日前一渔船在南海打渔时遇险,并立即拨打了求救电话,警方接到电话立即派出直升机前去营救.飞机在空中A点看到渔船C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见渔船C的俯角为45°,已知飞机的飞行速度为3150米/分.(参考数据:tan20°≈0.3,cos20°≈0.9,sin20°≈0.2)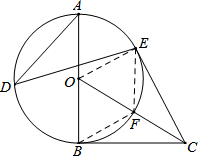 如图,以Rt△OBC的直角边OB为半径作⊙O,点D、E都在⊙O上,且∠ADE=∠OCB,连接CE.
如图,以Rt△OBC的直角边OB为半径作⊙O,点D、E都在⊙O上,且∠ADE=∠OCB,连接CE.