题目内容
20.计算:(1)(-66)×($\frac{1}{2}$-$\frac{1}{3}$+$\frac{5}{11}$) (2)4-(-3)2×2
(3)-22÷$\frac{2}{3}$×(1-$\frac{1}{3}$)2 (4)32÷(-$\frac{1}{3}$)3-24÷(-$\frac{1}{2}$)
分析 (1)原式利用乘法分配律计算即可得到结果;
(2)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果;
(3)原式先计算乘方运算,再计算乘除运算即可得到结果;
(4)原式先计算乘方运算,再计算除法运算,最后算加减运算即可得到结果.
解答 解:(1)原式=-33+22-30=-41;
(2)原式=4-18=-14;
(3)原式=-4×$\frac{3}{2}$×$\frac{4}{9}$=-$\frac{8}{3}$;
(4)原式=9×(-27)+16×2=-243+32=-211.
点评 此题考查了有理数的混合运算,以及乘法运算律,熟练掌握运算法则及运算律是解本题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
10.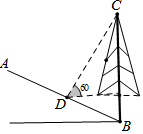 如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).
如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).
 如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).
如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).
8.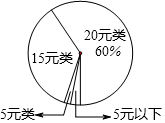 某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.
某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.
(1)求表中字母m的值及扇形统计图中“15元类”所对应的圆心角的度数.
(2)该校九年级共1200人,请估计捐款金额不低于15元的学生人数.
(3)据了解,样本中捐款金额为5元以下的同学的捐款金额为2元或1元,若从样本中捐款金额为5元以下的同学中随机抽取1位同学,求所抽同学的捐款金额为2元的概率.
 某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.
某校为了了解2015年九年级学生在某次为贫困山区小朋友的捐款情况,从中随机抽取了40名学生的捐款金额(元)进行统计分析.统计中发现这40名同学的捐款金额可分为20元、15元、5元、5元以下,并按捐款金额分为4类,各类的合计捐款数(元)如下表,各类的合计捐款数(元)如下扇形统计图.其中20元类的合计捐款数占这40名同学的总捐款数的60%.| 类别 | 20元类 | 15元类 | 5元类 | 5元以下 |
| 各类合计捐款数 | 360 | m | 5 | 10 |
(2)该校九年级共1200人,请估计捐款金额不低于15元的学生人数.
(3)据了解,样本中捐款金额为5元以下的同学的捐款金额为2元或1元,若从样本中捐款金额为5元以下的同学中随机抽取1位同学,求所抽同学的捐款金额为2元的概率.
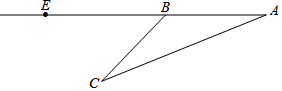 日前一渔船在南海打渔时遇险,并立即拨打了求救电话,警方接到电话立即派出直升机前去营救.飞机在空中A点看到渔船C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见渔船C的俯角为45°,已知飞机的飞行速度为3150米/分.(参考数据:tan20°≈0.3,cos20°≈0.9,sin20°≈0.2)
日前一渔船在南海打渔时遇险,并立即拨打了求救电话,警方接到电话立即派出直升机前去营救.飞机在空中A点看到渔船C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见渔船C的俯角为45°,已知飞机的飞行速度为3150米/分.(参考数据:tan20°≈0.3,cos20°≈0.9,sin20°≈0.2) 如图,∠A=∠D,∠ABC=∠DCB,求证:OA=OD.
如图,∠A=∠D,∠ABC=∠DCB,求证:OA=OD.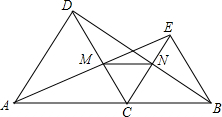 如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.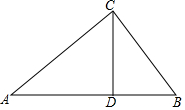 某景区把一块三角形的废地开辟为动物园,如图所示,测得AC=80m,BC=60m,AB=100m.
某景区把一块三角形的废地开辟为动物园,如图所示,测得AC=80m,BC=60m,AB=100m.