题目内容
3.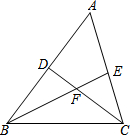 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )| A. | 118° | B. | 119° | C. | 120° | D. | 121° |
分析 根据角平分线的定义可得出∠CBF=$\frac{1}{2}$∠ABC、∠BCF=∠ACB,再根据内角和定理结合∠A=60°即可求出∠BFC的度数.
解答 解:∵∠ABC、∠ACB的平分线BE、CD相交于点F,
∴∠CBF=$\frac{1}{2}$∠ABC,∠BCF=$\frac{1}{2}$∠ACB,
∵∠A=60°,
∴∠ABC+∠ACB=180°-∠A=120°,
∴∠BFC=180°-(∠CBF+BCF)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=120°.
故选C.
点评 本题考查了三角形内角和定理,根据角平分线的定义结合三角形内角和定理求出角的度数是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知关于x的方程x2+1=$\frac{k}{x}$有一个正的实数根,则k的取值范围是( )
| A. | k<0 | B. | k≤0 | C. | k>0 | D. | k≥0 |
15.已知⊙O的半径为5cm,圆内两平行弦AB、CD的长分别为6cm、8cm,则弦AB、CD间的距离为( )
| A. | 1cm | B. | 7cm | C. | 7cm或1cm | D. | 4cm或3cm |
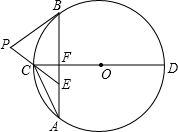 如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC,延长EC到点P,使PE=PB,连接AC,有下列四个结论:
如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC,延长EC到点P,使PE=PB,连接AC,有下列四个结论: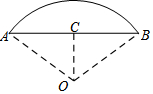 如图,弧AB的半径R为20m,AB的弦心距为OC为10m,求弓形的面积.
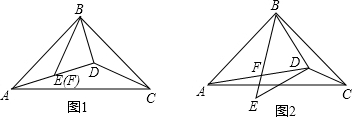
如图,弧AB的半径R为20m,AB的弦心距为OC为10m,求弓形的面积.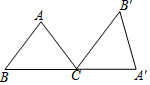 如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C.若点A′恰好落在BC的延长线上,则点B′到BA′的距离为$\frac{24}{5}$.
如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C.若点A′恰好落在BC的延长线上,则点B′到BA′的距离为$\frac{24}{5}$.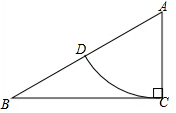 如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,以AC为半径画弧,交AB于D,则扇形CAD的周长是$\frac{π}{3}$+2(结果保留π)
如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,以AC为半径画弧,交AB于D,则扇形CAD的周长是$\frac{π}{3}$+2(结果保留π)