题目内容
11.已知:y=y1+y2,y1与x成正比例,y2与x-2成正比例,当x=1时,y=0;当x=3时,y=4.(1)求y与x之间的关系式;
(2)当x=-1时,求y的值.
分析 (1)设y1=ax,y2=k(x-2),由当x=1时,y=0.当x=3时,y=4可得关于a、k的两个等式联立方程组即可求出a,k,可得出y的表达式与x的函数关系式;
(2)然后把x=-3代入(1)的关系式中,求解即可.
解答 解:(1)设y1=ax,y2=k(x-2),
∴y=ax+k(x-2)
由当x=1时,y=0.当x=3时,y=4可得,
$\left\{\begin{array}{l}{0=a+k(1-2)}\\{\;}\\{4=3a+k(3-2)}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{\;}\\{k=1}\end{array}\right.$,
∴y与x之间的关系式为:y=2x-2;
(2)当x=-1时,y=2×(-1)-2=-4.
点评 本题考查了待定系数法求解析式以及求函数值,熟练掌握正比例函数的性质是关键.

练习册系列答案
相关题目
2.下列计算正确的是( )
| A. | 2-(-1)3=2-1=1 | B. | 74-4÷70=70÷70=1 | ||
| C. | $6÷({\frac{1}{3}-\frac{1}{2}})=6×3-6×2=6$ | D. | 23-32=8-9=1 |
19.己知△ABC中,∠C=Rt∠,AC=3,BC=4,点P为边AB的中点,以点C为圆心,长度r为半径画圆,使得点A,P在⊙O内,点B在⊙C外,则半径r的取值范围是( )
| A. | $\frac{5}{2}<r<4$ | B. | $\frac{5}{2}<r<3$ | C. | 3<r<4 | D. | r>3 |
16.杭州市用水收费规定如下:若每户每月的用水量不超过18立方米,则每立方米水价按2.9元收费,若用水量在18-25(含)立方米之间,则超过18立方米部分每立方米按3.85元收费,已知小静家1月份共交水费67.6元.若设小静家1月份用了x立方米的水,根据题意列出关于x的方程,正确的是( )
| A. | 3.85x=67.6 | B. | 18×2.9+3.85(x-18)=67.6 | ||
| C. | 18×2.9+3.85x=67.6 | D. | 18×2.9+3.85(25-x)=67.6 |
3.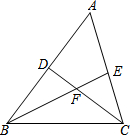 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )
 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )| A. | 118° | B. | 119° | C. | 120° | D. | 121° |
 一次函数y=kx+2(k为常数,且k≠0)的图象如图所示,则k的可能值为-2.(写一个即可)
一次函数y=kx+2(k为常数,且k≠0)的图象如图所示,则k的可能值为-2.(写一个即可) 如图,已知A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、…,则点A2016的坐标为(-504,-504).
如图,已知A1(1,0)、A2(1,1)、A3(-1,1)、A4(-1,-1)、A5(2,-1)、…,则点A2016的坐标为(-504,-504).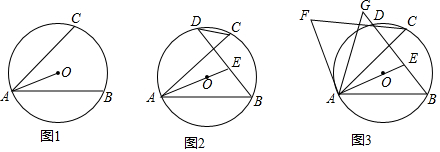
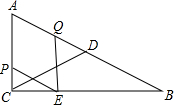 如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,CD是△ABC的中线,动点P从点C出发,沿CA以每秒1个单位长度的速度向终点A运动,同时,动点Q从点A出发,沿AB以每秒2个单位长度向终点B运动,过点P作PE∥AB,连结EQ,设点P运动的时间为t(s)(t>0)
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,CD是△ABC的中线,动点P从点C出发,沿CA以每秒1个单位长度的速度向终点A运动,同时,动点Q从点A出发,沿AB以每秒2个单位长度向终点B运动,过点P作PE∥AB,连结EQ,设点P运动的时间为t(s)(t>0)