题目内容
8.已知关于x的方程x2+1=$\frac{k}{x}$有一个正的实数根,则k的取值范围是( )| A. | k<0 | B. | k≤0 | C. | k>0 | D. | k≥0 |
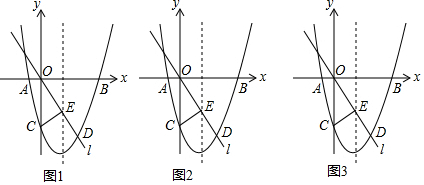
分析 将方程x2+1=$\frac{k}{x}$的解可看成抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点横坐标,画出函数图象,利用数形结合即可得出结论.
解答 解:方程x2+1=$\frac{k}{x}$的解可看成抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点横坐标.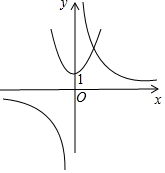
画出两函数图象,如图所示.
∵抛物线y=x2+1开口向上,且最低点为(0,1),
∴当x>0时,y=x2+1>0,
∴双曲线y=$\frac{k}{x}$在第一象限有图象,
∴k>0.
故选C.
点评 本题考查了二次函数的图象以及反比例函数的图象,依照题意画出图形,利用数形结合解决问题是解题的关键.

练习册系列答案
相关题目
19.己知△ABC中,∠C=Rt∠,AC=3,BC=4,点P为边AB的中点,以点C为圆心,长度r为半径画圆,使得点A,P在⊙O内,点B在⊙C外,则半径r的取值范围是( )
| A. | $\frac{5}{2}<r<4$ | B. | $\frac{5}{2}<r<3$ | C. | 3<r<4 | D. | r>3 |
16.杭州市用水收费规定如下:若每户每月的用水量不超过18立方米,则每立方米水价按2.9元收费,若用水量在18-25(含)立方米之间,则超过18立方米部分每立方米按3.85元收费,已知小静家1月份共交水费67.6元.若设小静家1月份用了x立方米的水,根据题意列出关于x的方程,正确的是( )
| A. | 3.85x=67.6 | B. | 18×2.9+3.85(x-18)=67.6 | ||
| C. | 18×2.9+3.85x=67.6 | D. | 18×2.9+3.85(25-x)=67.6 |
3.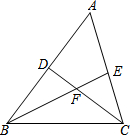 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )
 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=( )| A. | 118° | B. | 119° | C. | 120° | D. | 121° |
13.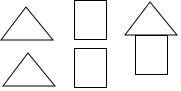 在拼图游戏中,从图的四张纸片中,任取两张纸片,能拼成“小房子”(如图)概率等于( )
在拼图游戏中,从图的四张纸片中,任取两张纸片,能拼成“小房子”(如图)概率等于( )
 在拼图游戏中,从图的四张纸片中,任取两张纸片,能拼成“小房子”(如图)概率等于( )
在拼图游戏中,从图的四张纸片中,任取两张纸片,能拼成“小房子”(如图)概率等于( )| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |